CONSTRUCTION OF INCENTER OF A TRIANGLE

Key Concept - Incenter

The point of concurrency of the internal angle bisectors of a triangle is called the incenter of the triangle and is denoted by I.

Before we learn how to  construct incenter of a triangle, first we have to learn how to construct angle bisector. 

So, let us learn how to construct angle bisector. 

Constructing Angle Bisector - Steps

To construct an angle bisector, you must need the following instruments.

1. Ruler

2. Compass

3. Protractor

The steps for the construction of an angle bisector are. 

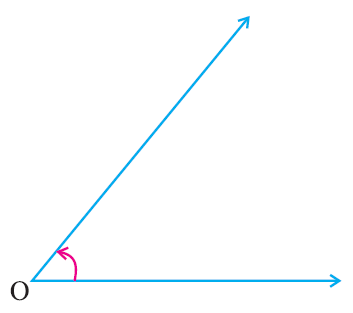
Step 1 :

Construct an angle of given measure at O using protractor.

Step 2 :

With ‘O’ as center draw an arc of any radius to cut the rays of the angle at A and B.

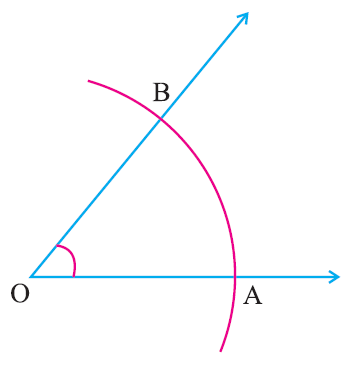
Step 3 :

With ‘A’ as center draw an arc of radius more than half of AB, in the interior of the given angle.

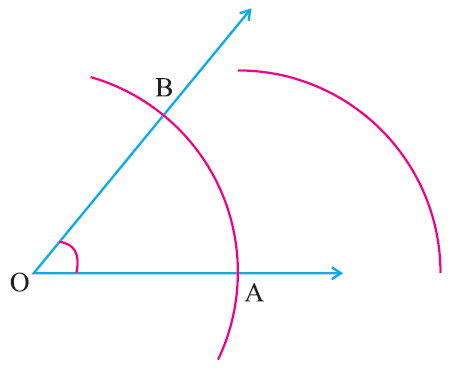
Step 4 :

With ‘B’ as center draw an arc of same radius to cut the previous arc at ‘C’.

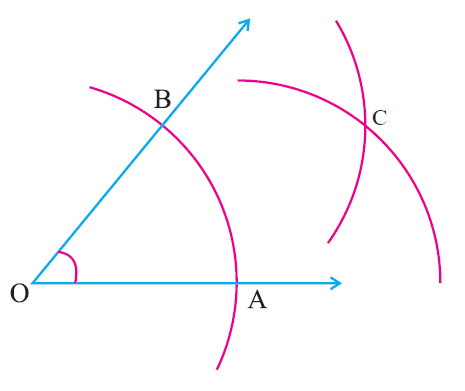
Step 5 :

Join OC.

OC is the angle bisector of the given angle.

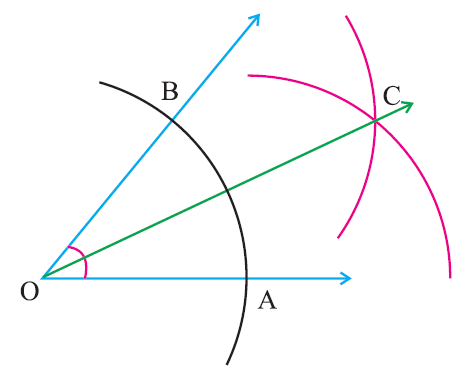
This construction clearly shows how to draw the angle bisector of a given angle with compass and straightedge or ruler. The angle bisector divides the given angle into two equal parts. 

For example, if we draw angle bisector for the angle 60°, the angle bisector will divide 60° in to two equal parts and each part will measure 30°.

Now, let us see how to construct incenter of a triangle. 

Construction of Incenter of a Triangle - Steps

To construct incenter of a triangle, we must need the following instruments.

1. Ruler

2. Compass

Let us see, how to construct incenter through the following example.  

Construct the incenter of the triangle ABC with AB = 7 cm, ∠B = 50° and BC = 6 cm. And also measure its radius.

Step 1 :

Draw triangle ABC with the given measurements.

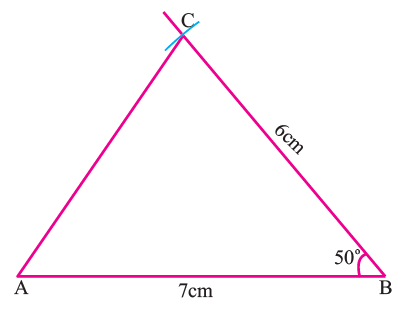
Step 2 :

Construct the angle bisectors of any two angles (A and B) and let them meet at I. 

In the above figure,  I is the incenter of triangle ABC.

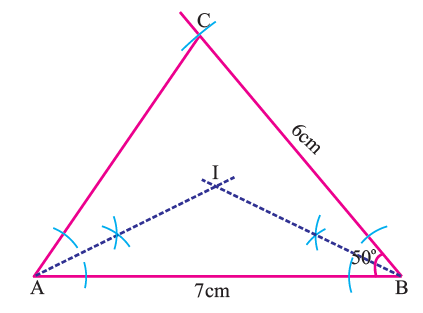
In the above figure,  I is the incenter of triangle ABC

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.