CONSTRUCTION OF FREQUENCY POLYGON WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Draw a frequency polygon imposed on the histogram for the following distribution
|
Class intervals 10 - 20 20 - 30 30 - 40 40 - 50 50 - 60 60 - 70 70 - 80 80 - 90 |
Frequency 4 6 8 10 12 14 7 5 |
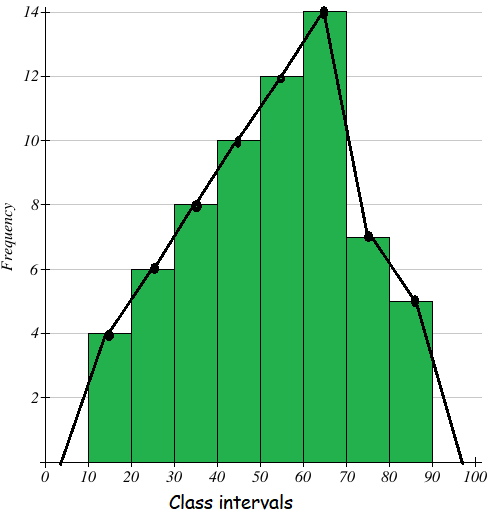
1. Answer :
|
Class intervals 10 - 20 20 - 30 30 - 40 40 - 50 50 - 60 60 - 70 70 - 80 80 - 90 |
Frequency 4 6 8 10 12 14 7 5 |
Take the class-intervals along the X-axis and frequencies along the Y-axis with appropriate scale as shown figure given below.
Draw a histogram for the given data. Now we have to mark the mid points of the upper sides of the consecutive rectangles. We also mark the midpoints of the assumed class intervals 0-10 and 90-100.
The mid points are joined with the help of a ruler. The ends of the polygon are joined with the mid points of 0-10 and 90-100.
Now, we get the frequency polygon.
Scale :
x - axis 1 cm = 10 units
y - axis 1 cm = 2 units
Problem 2 :
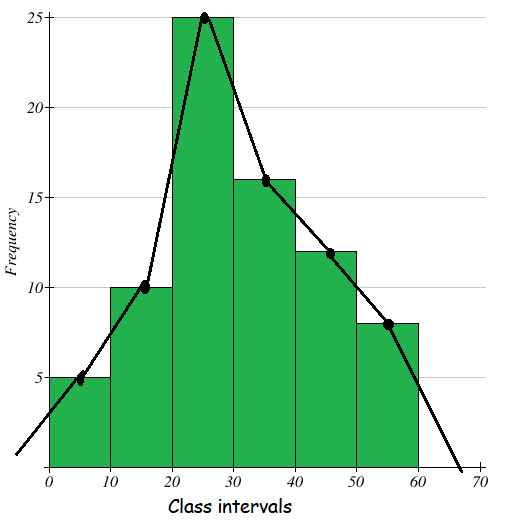
Draw a frequency polygon of the following data using histogram
|
Class intervals 0 - 10 10 - 20 20 - 30 30 - 40 40 - 50 50 - 60 |
Frequency 5 10 25 16 12 8 |
Solution :
Mark the class intervals along the X-axis and the frequencies along the Y-axis with appropriate scale shown in figure given below.
Draw a histogram for the given data. Now, mark the mid points of the upper sides of the consecutive rectangles. Also we take the imagined class interval (-10) - 0 and 60 - 70. The mid points are joined with the help of a ruler. The ends of the polygon are joined with the mid points of the imagined class intervals (-10)-0 and 60 - 70. Now we get the frequency polygon.
Sometimes imagined class intervals do not exist. For example, in case of marks obtained by the students in a test, we cannot go below zero and beyond maximum marks on the two sides.
In such cases, the extreme line segments are only partly drawn and are brought down vertically so that they meet at the mid points of the vertical left and right sides of first and last rectangles respectively.
Problem 3 :
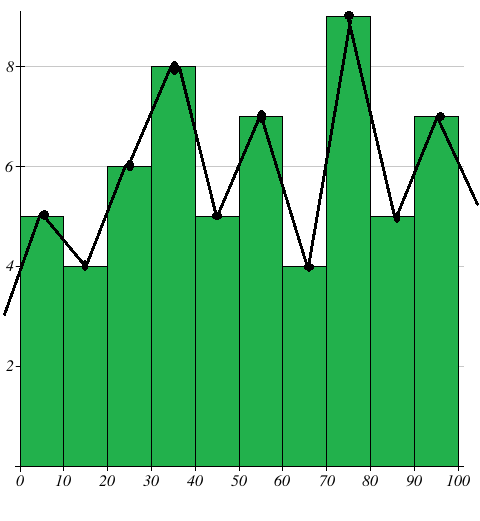
Draw a frequency polygon for the following data using histogram
|
Marks 0 - 10 10 - 20 20 - 30 30 - 40 40 - 50 50 - 60 60 - 70 70 - 80 80 - 90 90 - 100 |
Number of students 5 4 6 8 5 7 4 9 5 7 |
Solution :
Mark the class intervals along the X-axis and the number of students along the Y-axis. Draw a histogram for the given data. Now mark the mid points of the upper sides of the consecutive rectangles. The mid points are joined with the help of a ruler.
Note that, the first and last edges of the frequency polygon meet at the mid point of the vertical edges of the first and last rectangles.
Problem 4 :
Tia asked her friends how many times they visited the cinema last month. The frequency polygon shows her results.
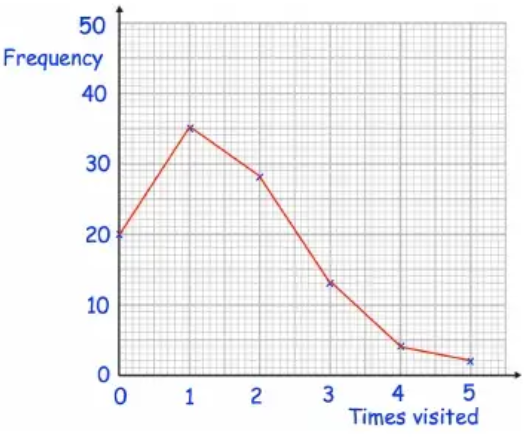
a) How many people visited the cinema twice ?
b) What is most popular number of times that her friends visited the cinema ?
c) What is the most number of times that somebody visited the cinema ?
d) How many people did Tia survey in total ?
Solution :
a) Number of people visited the cinema twice is 29.
b) 2 of her friends visited the cinema 5 times.
c) 35 people has visited once.
c)
Total = 20 + 35 + 29 + 14 + 4 + 2
= 104
So, total number of people visited is 104.
Problem 5 :
In one month, Janet travelled by bus 25 times and by train 25 times. The grouped frequency table records the number of minutes (x minutes) late each of her buses and trains were.
|
Minutes late 0 ≤ x < 5 5 ≤ x < 10 10 ≤ x < 15 15 ≤ x < 20 20 ≤ x < 25 |
Bus 5 15 4 1 0 |
Train 9 6 6 2 3 |
(a) On the grid below draw two frequency polygons to illustrate this data.
(b) Use your polygons to compare the lateness of buses and trains and comment on any differences you observe.
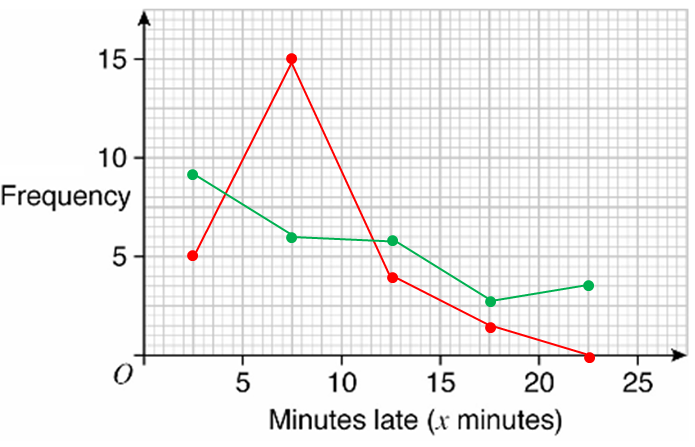
Solution :
|
Minutes late 0 ≤ x < 5 5 ≤ x < 10 10 ≤ x < 15 15 ≤ x < 20 20 ≤ x < 25 |
Midpoint 2.5 7.5 12.5 17.5 22.5 |
Bus 5 15 4 1 0 |
Train 9 6 6 2 3 |
Problem 6 :
The frequency table gives information about the times it took some office workers to get to the office one day.
|
Time (t minutes) 0 < t ≤ 10 10 < t ≤ 20 20 < t ≤ 30 30 < t ≤ 40 40 < t ≤ 50 50 < t ≤ 60 |
Frequency 4 8 14 16 6 2 |
(a) Draw a frequency polygon for this information.
(b) Write down the modal class interval.
One of the office workers is chosen at random.
(c) Work out the probability that this office worker took more than 40 minutes to get to the office
Solution :
a)
|
Time (t minutes) 0 < t ≤ 10 10 < t ≤ 20 20 < t ≤ 30 30 < t ≤ 40 40 < t ≤ 50 50 < t ≤ 60 |
Midpoint 5 15 25 35 45 55 |
Frequency 4 8 14 16 6 2 |
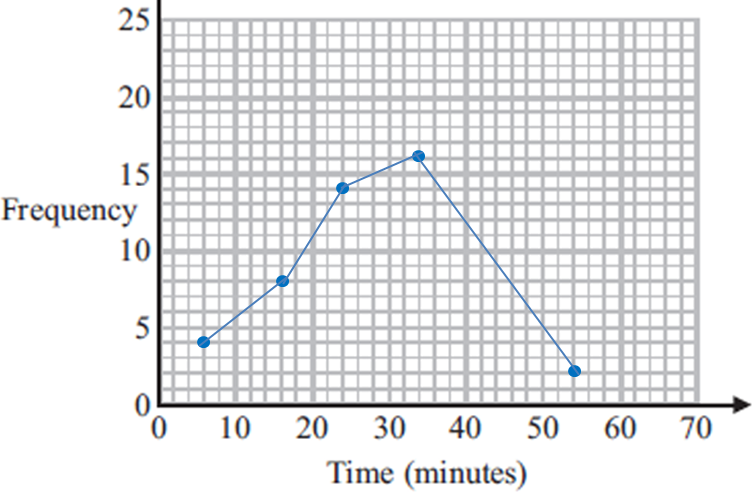
b) 30 < t ≤ 40 is the modal class
c) worker took more than 40 minutes to get to the office
= 6 + 2
= 8
Total = 4 + 8 + 14 + 16 + 6 + 2
= 50
Required probability = 8/50
= 4/25
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 1)
Feb 05, 26 09:37 AM
Digital SAT Math Problems and Solutions (Part - 1) -
AP Precalculus Problems and Solutions
Feb 05, 26 06:41 AM
AP Precalculus Problems and Solutions -
SAT Math Preparation with Hard Questions
Feb 05, 26 05:30 AM
SAT Math Preparation with Hard Questions

