CONGRUENT TRIANGLES ON A COORDINATE PLANE WORKSHEET

Problem 1 :

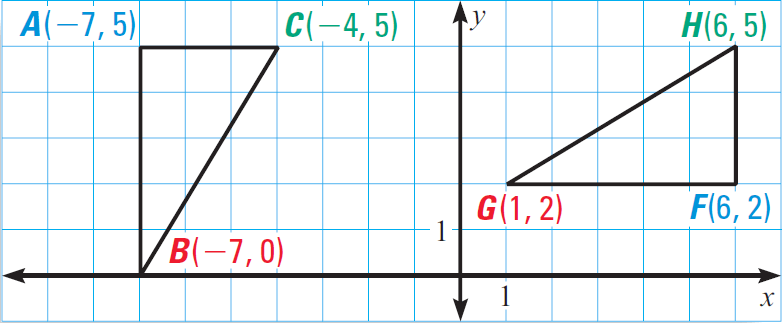
In the diagram given below, prove that ΔABC  ≅  ΔFGH.

Problem 2 :

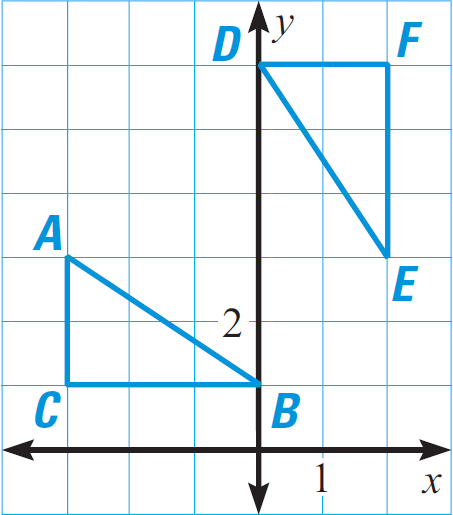
In the diagram given below, prove that ΔABC  ≅  ΔDEF. 

Problem 3 :

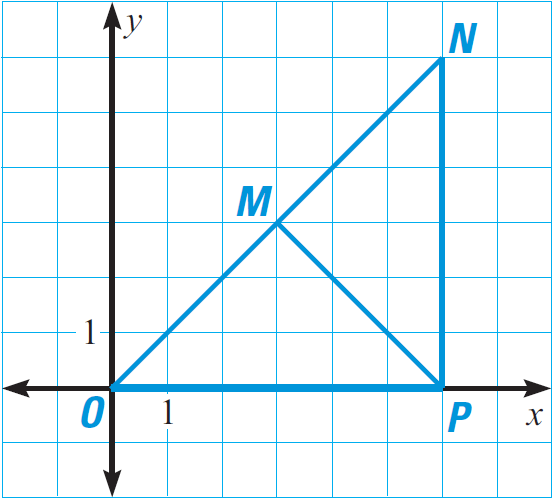
In the diagram given below, prove that ΔOPM  ≅  ΔMNP. 

Answers

1. Answer :

Because AB = 5 in triangle ABC and FG = 5 in triangle FGH, 

AB  ≅  FG.

Because AC = 3 in triangle ABC and FH = 3 in triangle FGH, 

AC  ≅  FH.

Use the distance formula to find the lengths of BC and GH. 

Length of BC : 

BC  =  √[(x₂ - x₁)² + (y₂ - y₁)²]

Here (x₁, y₁)  =  B(-7, 0) and (x₂, y₂)  =  C(-4, 5)

BC  =  √[(-4 + 7)² + (5 - 0)²]

BC  =  √[3² + 5²]

BC  =  √[9 + 25]

BC  =  √34

Length of GH : 

GH  =   √[(x₂ - x₁)² + (y₂ - y₁)²]

Here (x₁, y₁)  =  G(1, 2) and (x₂, y₂)  =  H(6, 5)

GH  =  √[(6 - 1)² + (5 - 2)²]

GH  =  √[5² + 3²]

GH  =  √[25 + 9]

GH  =  √34

Conclusion :

Because BC = √34 and GH = √34,

BC  ≅  GH

All the three pairs of corresponding sides are congruent. By SSS congruence postulate, 

ΔABC  ≅  ΔFGH

2. Answer :

From the diagram given above, we have

A(-3, 3), B(0, 1), C(-3, 1), D(0, 6), E(2, 3), F(2, 6)

Because AC = 2 in triangle ABC and DF = 2 in triangle DEF, 

AC  ≅  DF.

Because BC = 3 in triangle ABC and EF = 3 in triangle DEF, 

BC  ≅  EF.

Use the distance formula to find the lengths of BC and GH. 

Length of AB : 

AB  =   √[(x₂ - x₁)² + (y₂ - y₁)²]

Here (x₁, y₁)  =  A(-3, 3) and (x₂, y₂)  =  B(0, 1)

AB  =  √[(0 + 3)² + (1 - 3)²]

AB  =  √[3² + (-2)²]

AB  =  √[9 + 4]

AB  =  √13

Length of DE : 

DE  =  √[(x₂ - x₁)² + (y₂ - y₁)²]

Here (x₁, y₁)  =  D(0, 6) and (x₂, y₂)  =  E(2, 3)

DE  =  √[(2 - 0)² + (3 - 6)²]

DE  =  √[2² + (-3)²]

DE  =  √[4 + 9]

DE  =  √13

Conclusion :

Because AB = √13 and DE = √13,

AB  ≅  DE

All the three pairs of corresponding sides are congruent. By SSS congruence postulate, 

ΔABC  ≅  ΔDEF 

3. Answer :

PM is the common side for both the triangles OPM and MNP. 

Because OP = 6 in triangle OPM and PN = 6 in triangle MNP, 

OP  ≅  PN.

Use the distance formula to find the lengths of OM and MN. 

Length of OM : 

OM  =   √[(x₂ - x₁)² + (y₂ - y₁)²]

Here (x₁, y₁)  =  O(0, 0) and (x₂, y₂)  =  M(3, 3)

OM  =  √[(3 - 0)² + (3 - 0)²]

OM  =  √[3² + 3²]

OM  =  √[9 + 9]

OM  =  √18

Length of MN : 

MN  =   √[(x₂ - x₁)² + (y₂ - y₁)²]

Here (x₁, y₁)  =  M(3, 3) and (x₂, y₂)  =  N(6, 6)

MN  =  √[(6 - 3)² + (6 - 3)²]

MN  =  √[3² + 3²]

MN  =  √[9 + 9]

MN  =  √18

Conclusion :

Because  OM = √18 and MN = √18,

OM  ≅  MN

All the three pairs of corresponding sides are congruent. By SSS congruence postulate, 

ΔOPM  ≅  ΔMNP

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.