CONGRUENCE AND TRIANGLES

Two geometric figures are congruent if they have the exactly the same size and shape. Each of the red figure given below is congruent to other red figures. None of the blue figures is congruent to another blue figure.

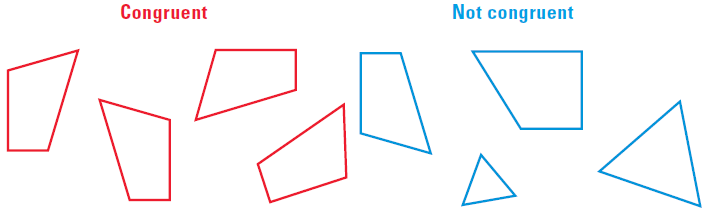
When two figures are congruent, there is a correspondence between their angles and sides such that corresponding angles are congruent and corresponding sides are congruent.

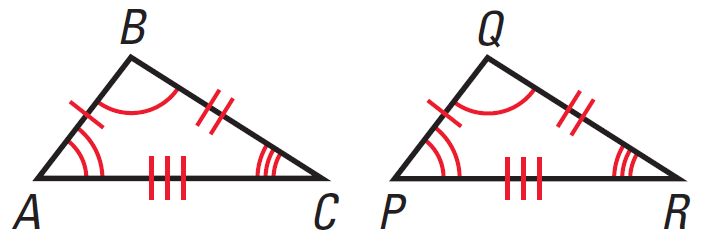
For the triangles below, we can write ΔABC ≅  ΔPQR, which is read "Triangle ABC is congruent to Triangle PQR". The notation shows the congruence and the correspondence.

There is more than one way to write a congruence statement, but it is important to list the corresponding angles in the same order. For example, we can write

ΔCAB ≅ ΔRPQ

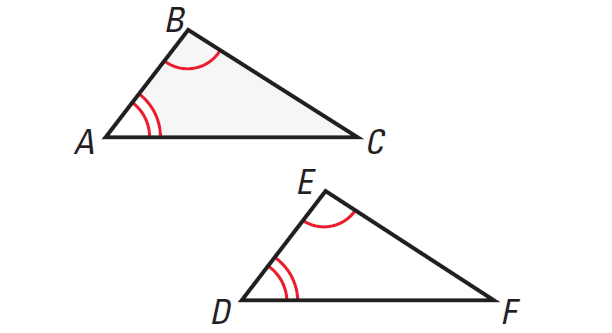
Third Angles Theorem

If two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.

In the diagram given below, if ∠A ≅ ∠D and ∠B ≅ ∠E, then ∠C ≅ ∠F.

Solving Problems on Congruence and Triangles

Problem 1 :

The congruent triangles represent the triangles in the diagram given below. Write a congruence statement. Identify all pairs of congruent corresponding parts.

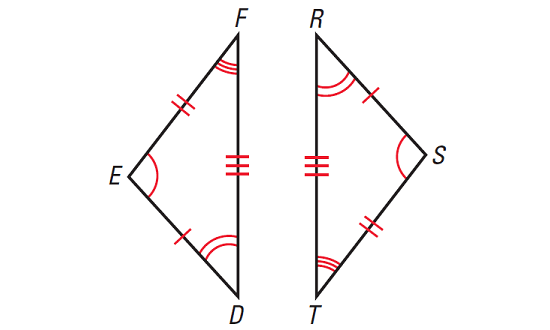
Solution :

The diagram indicates that ΔDEF ≅  ΔRST.

The congruent angles and sides are as follows.

Angles :

∠D ≅ ∠R, ∠E ≅ ∠S and ∠F ≅ ∠T

Sides :

DE ≅ RS, EF ≅ ST and FD ≅ TR

Problem 2 :

In the diagram given below, NPLM ≅ EFGH.

(i) Find the value of x.

(ii) Find the value of y.

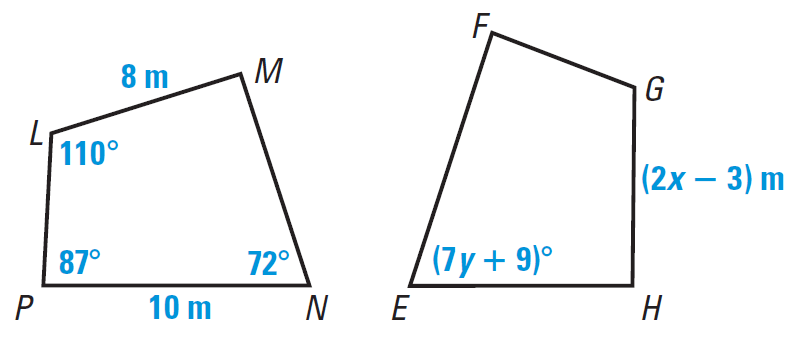
Solution (i) :

We know that LM ≅ GH.

So, we have

LM = GH

8 = 2x - 3

Add to 3 to both sides.

11 = 2x

Divide both sides by 2.

5.5 = x

Solution (ii) :

We know that ∠N ≅ ∠E.

So, we have

m∠N = m∠E

72° = (7y + 9)°

72 = 7y + 9

Subtract 9 from both sides.

63 = 7y

Divide both sides by 7.

9 = y

Problem 3 :

Find the value of x in the diagram given below.

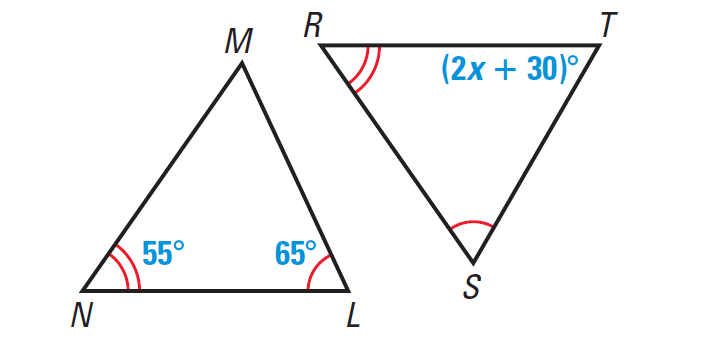
Solution :

In the diagram given above, ∠N ≅ ∠R and ∠L ≅ ∠S. From the Third angles theorem, we know that ∠M ≅ ∠T. So, m∠M = m∠T.

From the triangle sum theorem, we have

m∠L + m∠M + m∠N = 180°

65° + 55° + m∠M = 180°

120° + m∠M = 180°

Subtract 120° from both sides.

m∠M = 60° 

By Third angles theorem, we have

m∠M = m∠T

Substitute 60° for m∠M and (2x + 30)° for m∠M.

60° = (2x + 30)°

60 = 2x + 30

Subtract 30 from both sides.

30 = 2x

Divide both sides by 2.

15 = x

Problem 4 :

Decide whether the triangles are congruent. Justify your reasoning.

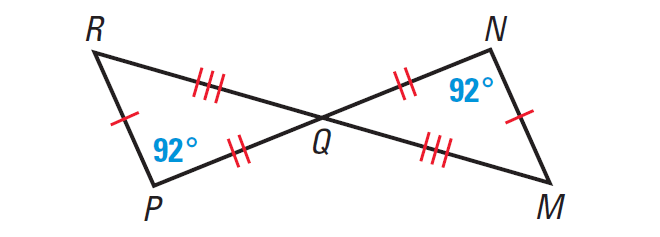
Solution :

From the diagram, we are given that all three pairs of corresponding sides are congruent.

RP ≅ MN, PQ ≅ NQ and QR ≅ QM

Because ∠P and ∠N have the same measure, ∠P ≅ ∠N.

By the Vertical Angles Theorem, we know that

ΔPQR ≅ ΔNQM

By the Third Angles Theorem,

∠R ≅ ∠M

So, all three pairs of corresponding sides and all three pairs of corresponding angles are congruent. By the definition of congruent angles,

ΔPQR ≅ ΔNQM

Problem 5 :

In the diagram given below, prove that ΔAEB ≅ ΔDEC.

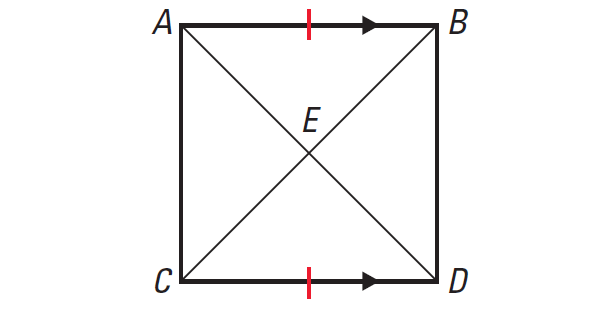
Solution :

Given :

AB || DC and AB ≅ DC

E is the midpoint of BC and AD

To prove :

ΔAEB ≅ ΔDEC

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.