CONDITIONAL TRIGONOMETRIC IDENTITIES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Trigonometric identities are true for all admissible values of the angle involved. There are some trigonometric identities which satisfy the given additional conditions. Such identities are called conditional trigonometric identities.
Example 1 :
If A + B + C = π/2, prove that
sin2A + sin2B + sin2C = 4cosAcosBcosC
Solution :
sin2A + sin2B + sin2C :
= 2sin(A + B)cos(A - B) + sin2C
= 2sin(90 - C)cos(A - B) + 2sinCcosC
= 2cosCcos(A - B) + 2sinCcosC
= 2cosC[cos(A - B) + sinC]
= 2cosC[cos(A - B) + sin(90 - (A + B)]
= 2cosC[cos(A - B) + cos(A + B)]
= 2cosC[2cosAcos(-B)]
= 2cosC[2cosAcosB]
= 4cosAcosBcosC
Example 2 :
If A + B + C = π/2, prove that
cos2A + cos2B + cos2C = 1 + 4sinAsinBcosC
Solution :
cos2A + cos2B + cos2C :
Use the identity of (cosC + cosD) for cos2A + cos2B.
= 2cos(A + B)cos(A - B) + cos2C
= 2cos(90 - C)cos(A - B) + 1 - 2sin2C
= 2sinCcos(A - B) + 1 - 2sin2C
= 1 + 2sinC[cos(A - B) - sinC]
= 1 + 2sinC[cos(A - B) - sin(90 - (A + B)]
= 1 + 2sinC[cos(A - B) - cos(A + B)]
= 1 + 2sinC[-2sinAsin(-B)]
= 1 + 2sinC[2sinAsinB]
= 1 + 4sinAsinBsinC
Example 3 :
If triangle ABC is a right triangle and ∠A = π/2, then prove that
(i) cos2B + cos2C = 1
(ii) sin2B + sin2C = 1
(iii) cosB - cosC = -1 + 2√2cos(B/2)sin(C/2)
Solution :
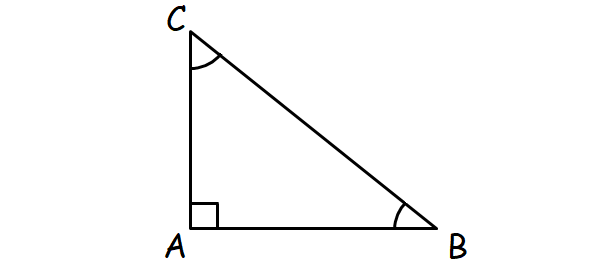
(i) cos2 B + cos2 C = 1 :
In the right triangle ABC above,
cosθ = Adjacent side/Hypotenuse
cosB = AB/BC
cosC = AC/BC
cos2B + cos2C = (AB/BC)2 + (AC/BC)2
= (AB2 + AC2)/BC2
= BC2/BC2
= 1
(ii) sin2 B + sin2 C = 1 :
In the right triangle ABC above,
sinθ = Opposite side/Hypotenuse
sinB = AC/BC
sinC = AB/BC
sin2B + sin2C = (AC/BC)2 + (AB/BC)2
= AC2/BC2 + (AB2/BC2)
= (AC2 + AB2)/BC2
= BC2/BC2
= 1
(iii) cosB − cosC = -1 + 2 √2 cos B/2 sin C/2 :
cosB - cosC = 2cos2B - 1 - cosC
= -1 + 2cos2B - cosC ----(1)
In the triangle ABC above,
A + B + C = π
It is given that A = π/2. Then,
B + C = π/2
C = π/2 - B
Substitute C = π/2 - B in (1).
= -1 + 2cos2(B/2) - cos(π/2 - B)
= -1 + 2cos2(B/2) - sinB
= -1 + 2cos2(B/2) - 2sin(B/2)cos(B/2)
= -1 + 2cos(B/2)(cos(B/2) - sin(B/2))
B = π/2 - C ----> B/2 = π/4 - C/2
= -1 + 2cos(B/2)[cos(π/4 - C/2) - sin(π/4 - C/2)]
= -1 + 2cos(B/2)[cos(π/4 - C/2) - cos(π/2 - (π/4 - C/2))]
= -1 + 2cos(B/2)[cos(π/4 - C/2) - cos(π/4 + C/2)]
= -1 + 2cos(B/2)[-2sin(π/4)sin(-C/2)]
= -1 + 2cos(B/2)[2(1/√2)sin(C/2)]
= -1 + 2√2cos(B/2)sin(C/2)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 50)
Mar 06, 26 07:48 PM
Digital SAT Math Problems and Solutions (Part - 50) -
Digital SAT Math Problems and Solutions (Part - 49)
Mar 06, 26 06:47 PM
Digital SAT Math Problems and Solutions (Part - 49) -
Digital SAT Math Problems and Solutions (Part - 48)
Mar 06, 26 05:24 PM
Digital SAT Math Problems and Solutions (Part - 48)


