HOW TO CHECK IF 3 LINES ARE CONCURRENT
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Concurrent Lines
If three are more straight lines intersect at a common point, then the lines are said to be concurrent lines.
Point of Concurrency
The common point at where the lines are intersecting is called point of concurrency.
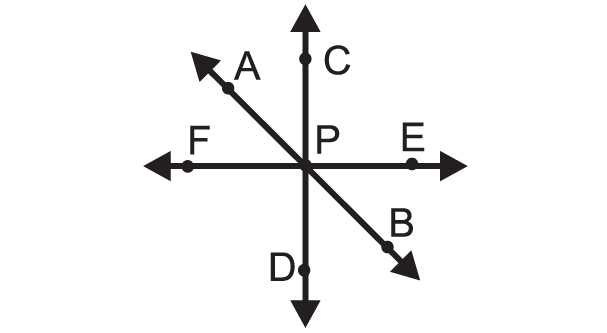
In the figure above, the lines AB, CD and EF are concurrent lines, as they all intersect at a common point P. And, P is the point of concurrency.
How to Check if Three Lines are Concurrent
Method 1 :
(i) Solve any two of the givem equations and obtain point of intersection.
(ii) Substitute the point into the third equation and check, if the point satisfies the third equation.
(iv) If the point satisfies the third equation, then the three lines are concuurent.
Method 2 :
Consider the equations of three lines in general form as shown below.
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
a3x + b3y + c3 = 0
If the above three lines are concurrent, then the coefficients of x, y and the constant terms must satisfy the following condition.
To get the point of concurrency, solve any two of the given three equations.
Example 1 :
Show that the following straight lines are concurrent and find the point of concurrency.
2x - 3y + 4 = 0
9x + 5y = 19
2x -7y + 12 = 0
Solution :
2x - 3y + 4 = 0 ----(1)
9x + 5y - 19 = 0 ----(2)
2x -7y + 12 = 0 ----(3)
5(1) - 3(2) :
37x = 37
x = 1
Substitute x = 1 into (1).
2(1) - 3y + 4 = 0
2 - 3y + 4 = 0
-3y + 6 = 0
-3y = -6
y = 2
The point of interesection of (1) and (2) is (1, 2).
Substitute the point (1, 2) into (3).
2(1) - 7(2) + 12 = 0
2 -14 +12 = 0
-12 + 12 = 0
0 = 0 (true)
The point (1, 2) satisfies (3). So, the point (1, 2) lies on the third line.
Therefore, the given three lines are concurrent and the point of concurrency is (1, 2).
Example 2 :
Show that the following straight lines are concurrent and find the point of concurrency.
3x + 4y = 13
2x - 7y = -1
5x - y = 14
Solution :
Write the given equations in general form.
3x + 4y - 13 = 0 ----(1)
2x - 7y + 1 = 0 ----(2)
5x - y - 14 = 0 ----(3)
Find the value of the determinant with the coefficients of x, y and constant terms as explained in Method 2 above.
= 3(98 + 1) - 4(-28 - 5) - 13(-2 + 35)
= 3(99) - 4(-33) - 13(33)
= 297 + 132 - 429
= 429 - 429
= 0
Since the value of the determinant is zero, the given lines are concurrent.
Solve any two of (1), (2) and (3) to find the point of concurrency.
2(1) - 3(2) :
29y = 29
y = 1
Substitute y = 1 into (1).
3x + 4(1) - 13 = 0
3x + 4 - 13 = 0
3x - 9 = 0
3x = 9
x = 3
The point of concurrency is (3, 1).
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation -
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37)


