CONCENTRIC CIRCLES

When a small stone was dropped in still water, you might have seen circular ripples were formed. Which is the center of these circles ?  

Is it not the place where the stone was dropped ?

Yes.

The circles with different measures of radii and with the same center are called concentric circles. The center is known as common center.

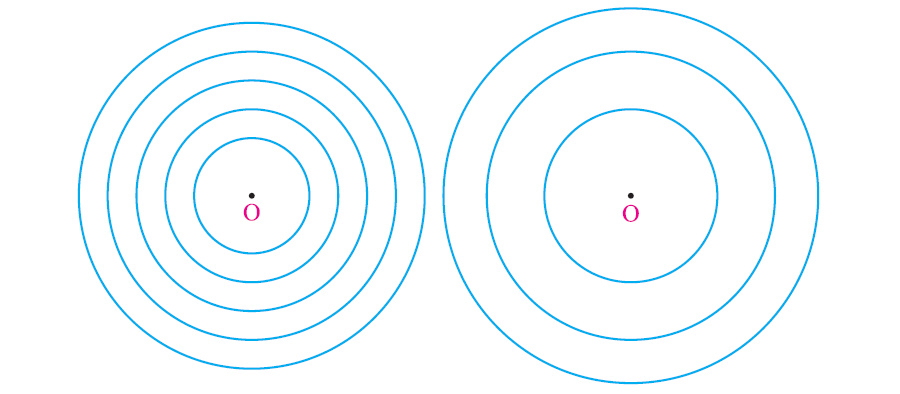
Circles drawn in a plane with a common center and different radii are called concentric circles. See the figure above.

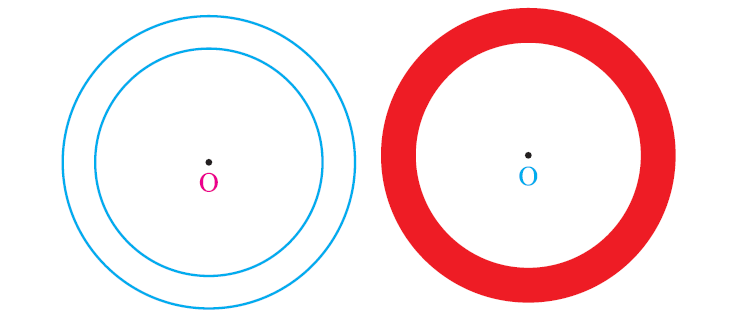
The above figure represents two concentric circles and the area between the two concentric circles is shaded in red color.

The red colored area is known as circular ring.

Circular Ring

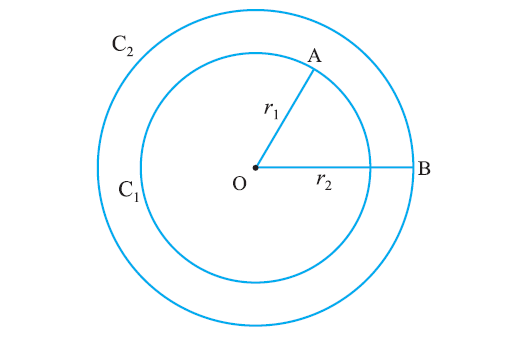
In the figure given above, C₁ and C₂ are two circles having the same center O with different radii r₁ and r₂  respectively.

Circles C₁ and C₂ are called concentric circles.

The area bounded between the two circles is known as circular ring.

Width of the circular ring : 

= OB – OA

= r₂  - r₁

where r₂ > r₁.

Construction of Concentric Circles

Example :

Draw concentric-circles with radii 3 cm and 5 cm and shade the circular ring. Find its width.

Solution :

Given: The radii are 3 cm and 5 cm.

Step 1 :

Draw a rough diagram and mark the given measurements.

Step 2 :

Take any point O and mark it as the center.

Step 3 :

With O as center and draw a circle of radius OA = 3 cm

Step 4 :

With O as center and draw a circle of radius OB = 5 cm.

Thus the concentric-circles C₁ and C₂ are drawn.

Width of the circular ring = OB – OA

= 5 – 3

= 2 cm

Calculate the shaded area of each shape below.

Problem 1 :

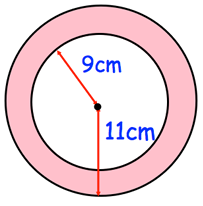
Solution :

Area of shaded region = Area of large circle - area of small circle

= πR² - πr²

R = 11 cm and r = 9 cm

= π(11)² - π(9)²

= π(121 - 81)

= π(40)

= 3.14(40)

= 125.6 cm²

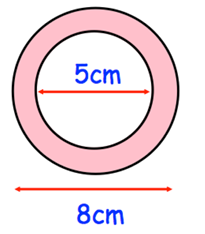
Problem 2 :

Solution :

Area of shaded region = Area of large circle - area of small circle

= πR² - πr²

R = 8/2 ==> 4 cm and r = 5/2 ==> 2.5 cm

= π(4)² - π(2.5)²

= π(16 - 6.25)

= π(9.75)

= 3.14(9.75)

= 30.615 cm²

Problem 3 :

A jewelry designer is making a pendant. The pendant will be a circular disc (center O) with a circular hole cut out of it, as shown. The radius of the disc is 35 millimeters. Find the area of the pendant

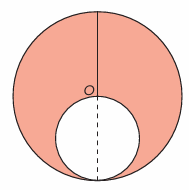
Solution :

Radius of disc = 35 mm ==> 3.5 cm

Diameter of the hole = 35 mm

radius = 3.5/2 cm

= 1.75 cm

Area of large circle - area of small circle

= π(3.5)² - π(1.75)²

= π(12.25 - 3.0625)

= π(8.9375)

= 3.14(8.9375)

= 28.06 cm²

Problem 4 :

A park is shaped like a rectangle with a semicircle on one end, and another semicircle cut out of one side.

a) Find the distance around the park.

b) Find the area of the park. Use 22/7 as an approximation for π.

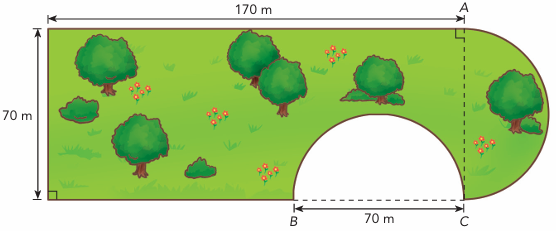
Solution :

a) Length around the shape

= 70 + 170 + πr + (170 - 70) + πr

Radius of semicircle = 70/2 ==> 35 m

= 70 + 170 + 2(3.14) (35) + 100

= 240 + 219.9 + 100

= 559.8 m

b)  Area of the park

= Area of rectangle + area of semicircle

= length x width + (1/2)πr²

= 170 x 70 + (1/2)(22/7) (35)²

= 170 x 70 + (1/2)(22/7) (35)²

= 11900 + 1925

= 13825 m²

Problem 5 :

The diameter of a circular fountain in a city park is 28 feet. A sidewalk that is 3.5 feet will be built around the fountain. Use

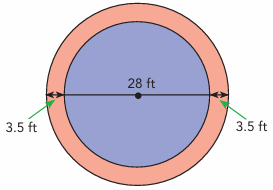
a) Find the area of the sidewalk. 22/7 as an approximation for π.

b) 0.8 bag of concrete will be needed for every square foot of the new sidewalk. What is the minimum number of bags needed?

Solution :

a) Diameter of circular park = 28 ft

radius = 14 ft

width = 3.5 ft

required radius = 14 + 3.5

= 17.5 ft

Area of sidewalk = πr²

= (22/7) x 17.5²

= 962.5 ft²

b) To cover 1 square ft, we need 0.8 bag

Required number of bags required = 962.5/0.8

= 1203.125

Approximately 1203 bags.

Problem 6 :

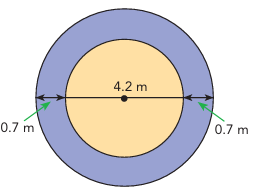
A water fountain shoots up a jet of water. The water falls back down onto the ground in the shape of a circle. Michelle wants the circle of water on the ground to be 0.7 meter wider on each side. She gradually increases the strength of the water jet. The area of the circle of water increases at 0.2 square meter per second.

Use 22/7 as an approximation for π.

a) Find the area of the original circle of water.

b) Find the area of the larger circle of water.

Solution :

a)  Area of original circle = πr²

r = 4.2/2 ==> 2.1 m

= π(2.1)²

= 13.86 square meter

b) area of large circle = r = 2.1 + 0.7 

= 2.8 m

= π(2.8)²

= 24.64 square meter

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.