CONCAVITY AND POINTS OF INFLECTION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Concave up :
The graph is said to be concave up (convex down) at a point if the tangent line to the graph at that point lies below the graph in the vicinity of the point.
Concave down :
It is said to be concave down (convex up) at a point if the tangent line lies above the graph in the vicinity of the point.
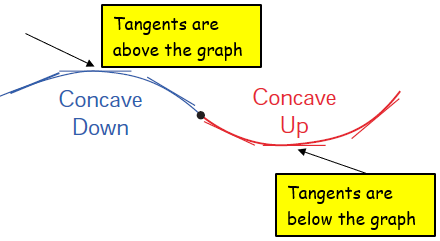
Relationship Between First Derivative and Concavity
Let f(x) be a function whose second derivative exists in an open interval I = (a, b). Then the function is said to be
(i) If f'(x) is strictly increasing on I, then the function is concave up on the open interval I.
(ii) If f'(x) is strictly decreasing on I, then the function is concave down on the open interval I.
Finding Concavity from Second Derivative
(i) If f''(x) > 0 on an open interval I, then f(x) is concave up on I.
(i) If f''(x) < 0 on an open interval I, then f(x) is concave down on I.
Point of Inflection
The points where the graph of the function changes from “concave up to concave down” or “concave down to concave up” are called the points of inflection of f (x) .
How to calculate point of inflection ?
(i) If f ′′(c) exists and f ′′(c) changes sign when passing through x = c , then the point
(c, f (c)) is a point of inflection of the graph of f .
(ii) If f ′′(c) exists at the point of inflection, then f ''(c) = 0 .
Inflection point and sharp point :
To determine the position of points of inflexion on the curve y = f (x) it is necessary to find the
points where f ′′(x) changes sign. For ‘smooth’ curves (no sharp corners), this may happen when either
(i) f ''(x) = 0 or
(ii) f ′′(x) does not exist at the point.
Problem 1 :
Find intervals of concavity and points of inflexion for the following functions:
(i) f (x) = x(x − 4)3
Solution :
f(x) = x(x − 4)3
u = x, v = (x − 4)3
u' = 1 and v' = 3(x-4)2
f'(x) = x[3(x-4)2] + (x − 4)3 (1)
f'(x) = (x-4)2[3x + (x−4)]
f'(x) = (x-4)2(4x-4)
u = (x-4)2 v = (4x-4)
u' = 2(x-4) and v' = 4
f''(x) = (x-4)2(4)+(4x-4)2(x-4)
f''(x) = (x-4)[4(x-4)+2(4x-4)]
f''(x) = (x-4)[4x-16+8x-8]
f''(x) = (x-4)(12x-24)
f''(x) = 12(x-4)(x-2)
f''(x) = 0
x - 4 = 0 and x - 2 = 0
x = 4 and x = 2
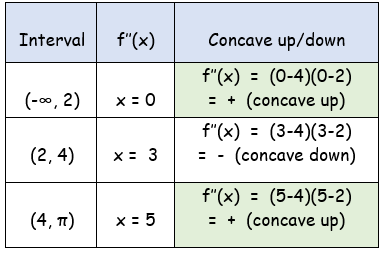
At x = 2, the curve changes its sign, it changes from concave up to concave down.
At x = 4, the curve changes its sign, it changes from concave down to concave up.
Point of inflection :
|
At x = 2 f (2) = 2(2 − 4)3 f (2) = 2(−2)3 f (2) = -16 |
At x = 4 f (4) = 2(4 − 4)3 f (4) = 0 |
So, point of inflection are (2, -16) and (4, 0).
(ii) y = sin x + cos x, 0 < x < 2π
Solution :
y = sin x + cos x
y' = cos x - sin x
y'' = -sinx -cosx
y'' = 0
-sinx -cosx = 0
-sinx = cosx
sinx/cosx = -1
tan x = -1
x = tan-1(-1)
x = 3π/4, 7π/4
The intervals are (0, 3π/4) (3π/4, 7π/4) and (7π/4, 2π).
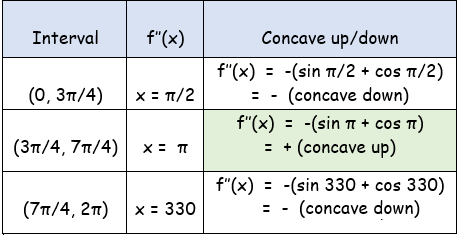
At x = 3π/4, the curve changes its sign, it changes from concave down to concave up.
At x = 7π/4, the curve changes its sign, it changes from concave up to concave down.
Point of inflection :
|
f(3π/4) = sin (3π/4) + cos(3π/4) = -1/√2 + 1/√2 = 0 |
f(7π/4) = sin (7π/4) + cos(7π/4) = -1/√2 + 1/√2 = 0 |
So, points of inflection are (3π/4, 0) and (7π/4, 0).
Problem 3 :
f(x) = 1/2 (ex-e-x)
Solution :
f(x) = 1/2 (ex-e-x)
f'(x) = 1/2 (ex+e-x)
f''(x) = 1/2 (ex-e-x)
f''(x) = 0
1/2 (ex-e-x) = 0
ex = e-x
e2x = 1
2x = 0
x = 0
So, the intervals are (-∞, 0) and (0, ∞).
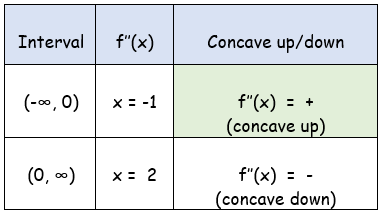
Point of Inflection :
at x = 0
f(0) = 0
So, point of inflection is (0, 0)
Problem 4 :
What are the coordinates of the points of inflection for the graph of f(x) = sin2x on the closed interval [0, π] ?
a) x = 3π/4 only
b) x = π/4, x = π/2 and x = 3π/4
c) x = π/4 and x = 3π/4
d) x = π/2 e) x = π/4
Solution :
f(x) = sin2x
f'(x) = 2 sin x cos x
= sin 2x
To find point of inflection, we have to equate the second derivative to 0.
f'(x) = sin 2x
f''(x) = cos 2x (2)
f''(x) = 2 cos 2x
f''(x) = 0
2 cos 2x = 0
2x = cos-1(0)
2x = π/2, 3π/2
x = π/4, 3π/4
So, in the interval [0, π] the given function has point of inflection at the point x = π/4 and 3π/4. So, option c is correct.
Problem 5 :
The function g is defined by the equation
g(x) = 6x5 - 10x3
Determine the values of x for which the graph of function g is concaved upwards
a) x > 1/2 b) -√2/2 < x < 0 or x > √2/2
c) -1/2 < x < 0 or x > 1/2 d) -1/2 < x < 1/2
e) -√2/2 < x < √2/2
Solution :
g(x) = 6x5 - 10x3
g'(x) = 30x4 - 30x2
g''(x) = 120x3 - 60x
g''(x) = 0
120x3 - 60x = 0
60x(2x2 - 1) = 0
x = 0 and 2x2 - 1 = 0
2x2 = 1
x2 = 1/2
x = -1/√2 and x = 1/√2
-1/2 < x < 0
When x = -0.4
f''(-0.4) = 60(-0.4)(2(-0.4)2 - 1)
= -24(0.32 - 1)
= -24(-0.68)
= + > 0
Concave up.
0 < x < 1/2
When x = 0.4
f''(0.4) = 60(0.4)(2(0.4)2 - 1)
= 24(0.32 - 1)
= 24(-0.68)
= - < 0
Concave down
x > 1/2
When x = 1
f''(1) = 60(1)(2(1)2 - 1)
= 60(2 - 1)
= + > 0
Concave up
The function is concave up in the intervals
-1/2 < x < 0 or x > 1/2
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
