COMPOUND AND ABSOLUTE VALUE INEQUALITIES

Two or more inequalities that are connected by the words and or or are called a compound inequality. A compound inequality containing and is true only if both inequalities are true. Its graph is the intersection of the graphs of the two inequalities. A compound inequality containing or is true if one or more of the inequalities is true. Its graph is the union of the graphs of the two inequalities.

Since the absolute value of any number x is its distance from zero on a number line, |x| < 1 means that the distance from zero to x is less than 1 unit and |x| > 1 means that the distance from zero to x is greater than 1 unit. Therefore the inequality |x| < 1 is equivalent to

-1 < x < 1

And |x| > 1 is equivalent to x < -1 or x > 1.

Graph of |x| < 1 :

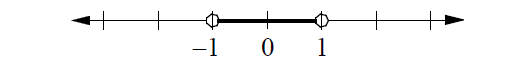
In the graph above, the distance between x and 0 is less than 1.

Graph of |x| > 1 :

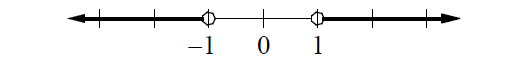
In the graph above, the distance between x and 0 is greater than 1.

To translate more general absolute value inequalities into compound inequalities, use the following properties.

1. The inequality |ax + b| < c is equivalent to

-c < ax + b < c,

in which c ≥ 0.

2. The inequality |ax + b| > c is equivalent to

ax + b < -c  or  ax + b > c,

in which c ≥ 0.

Note :

If you multiply or divide both sides of an inequality by the same negaive number, you have to flip the inequality sign.

Examples :

1 < 2 ----> 1 ⋅ (-1) > 2 ⋅ (-1) ----> -1 > -2

2 < 3 ----> ²⁄₍₋₁₎ > ³⁄₍₋₁₎ ----> -2 > -3

Solved Problems

Problem 1-4 : Solve for x.

Problem 1 :

7 - 2x > 15

Solution :

7 - 2x > 15

Subtract 7 from both sides.

-2x > 8

Divide both sides by -2.

x < -4

Problem 2 :

10 + 3x > -11

Solution :

10 + 3x > -11

Subtract 10 from both sides.

3x > -21

Divide both sides by 3.

x > -7

Problem 3 :

|2x - 3| ≤ 7

Solution :

|2x - 3| ≤ 7

-7 ≤ 2x - 3 ≤ 7

-4 ≤ 2x ≤ 10

-2 ≤ x ≤ 5

Problem 4 :

|x - 4| > 3

Solution :

x - 4 < -3  or  x - 4 > 3

x < 1  or  x > 7

Problem 5 :

3 - x < -2  or  2x + 3 ≤ -1

Which of the following numbers is NOT a solution to the above compound inequality?

(A)  -6

(B)  -2

(C)  2

(D)  6

Solution :

3 - x < -2  or  2x + 3 ≤ -1

x > 5  or  x ≤ -2

In option (C), 2 is not a solution to the given compound inequality.

Therefore, the correct answer is option (C).

Problem 6 :

5x + 7 > 2  and  6x - 15 ≤ 3(-1 + x)

Which of the following numbers is a solution to the above compound inequality?

(A)  -1

(B)  2

(C)  5

(D)  8

Solution :

x > -1  and  x ≤ 4

2 is a solution to the above compound inequality.

Therefore, the correct answer is option (B).

Problem 7 :

Which of the following is the graph of

-x ≤ 5  and  7 - (½)x > x + 1

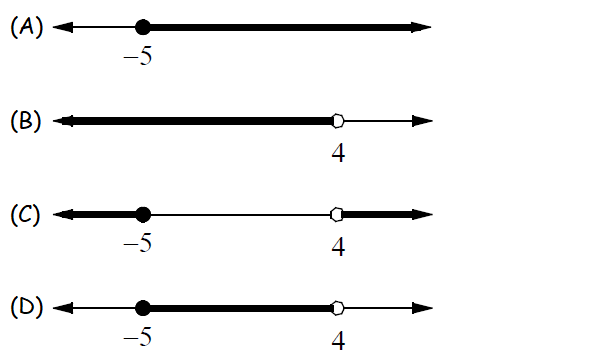
Solution :

-x ≤ 5  and  7 - (½)x > x + 1

x ≥ -5  and  x < 4

Problem 8 :

If -2 < x < -1, what is the value of 7 + (½)x rounded to the nearest whole number?

Solution :

-2 < x < -1

(½)(-2) < (½)x < (½)(-1)

7 - 1 < 7 + (½)x < 7 -½

6 < 7 + (½)x < 6½

6 < 7 + (½)x < 6.5

7 + (½)x rounded to the nearest whole number is 6.

Problem 9 :

Which of the following numbers is NOT a solution to the inequality |0.5x - 1| ≤ 1?

(A)  0

(B)  2

(C)  4

(D)  6

Solution :

|0.5x - 1| ≤ 1

-1 ≤ 0.5x ≤ 1

2(-1) ≤ 2(0.5x) ≤ 2(1)

-2 ≤ x ≤ 2

6 is not a solution to the given inequality.

Therefore, the correct answer is option (D).

Problem 10 :

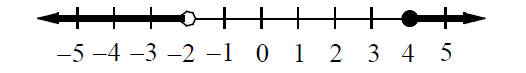
Which of the following is the compound inequality for the graph above?

(A)  x < -2  or  4 ≤ x

(B)  x ≤ -2  or  4 < x

(C)  -2 < x ≤ 4

(D)  -2 ≤ x < 4

Solution :

The compound inequality x < -2 or 4 ≤ x represents the graph above.

Therefore, the correct answer is option (A).

Problem 11 :

If (¼)x - 1 ≤ -x + 5, what is the greatest possible value of x?

Solution :

(¼)x - 1 ≤ -x + 5

4[(¼)x - 1] ≤ 4[-x + 5]

x - 4 ≤ -4x + 20

5x - 4 ≤ 20

5x ≤ 24

x ≤ ²⁴⁄₅

The greatest possible value of x is ²⁴⁄₅.

Problem 12 :

If |(¾)x - 2| < 1 and x is an integer, what is one possible value of x?

Solution :

|(¾)x - 2| < 1

-1 < (¾)x - 2 < 1

1 < (¾)x < 3

4 < 3x < 12

⁴⁄₃ < x < 4

⁴⁄₃ ≈ 1.33....

In the above inequality, the possible integer values for x are 2 and 3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.