COMPLEX PLANE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The complex plane, also known as the Argand plane, is a fundamental concept in complex analysis and provides a geometric representation of complex numbers. In the complex plane, each complex number is represented as a point with coordinates based on its real and imaginary parts.
A complex number z = x + iy is uniquely determined by an ordered pair of real numbers (x, y).
The numbers 2 -7i, 5, and -3i can be equated to the points as shown below.
2 - 7i = (2, -7)
5 = (9, 0)
-3i = (0, -3)
In this way, we can associate a complex number z = x + iy with a point (x, y) in a coordinate plane.
If we consider horizontal axis or x-axis as real axis and vertical axis or y-axis as imaginary axis to represent a complex number, then the xy-plane is called complex plane or Argand plane, which is named after the Swiss mathematician Jean Argand (1768 – 1822).
A complex number is represented not only by a point, but also by a position vector pointing from the origin to the point. The number, the point, and the vector will all be denoted by the same letter z . As usual we identify all vectors which can be obtained from each other by parallel displacements.
In real analysis, C denotes the set of all complex numbers. Geometrically, a complex number can be viewed as either a point in R2 or a vector in the Argand plane.
Complex number as a point :
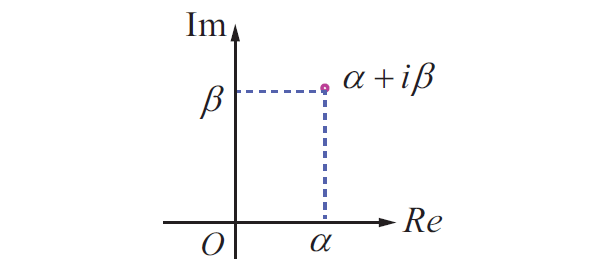
Complex number by a position vector pointing from the origin to the point :
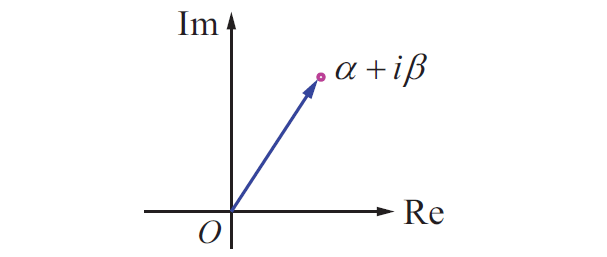
Complex number as a vector :
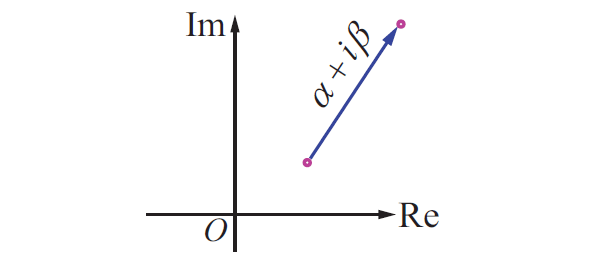
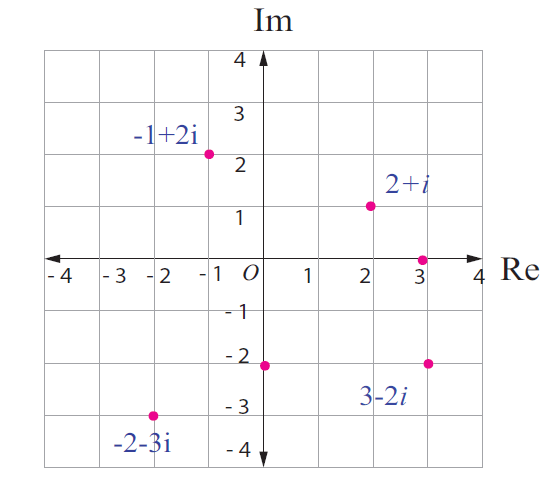
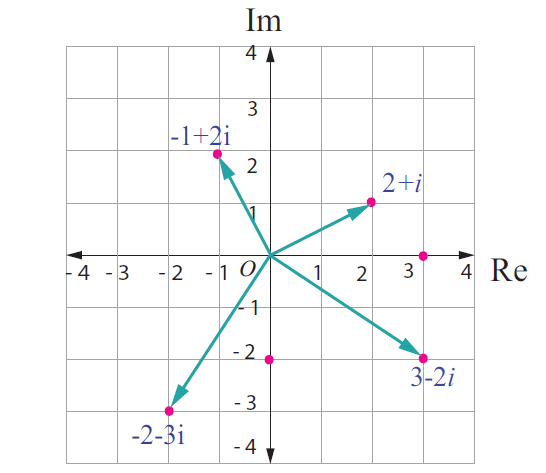
Here are some complex numbers :
2 + i
-1 + 2i
3 - 2i
0 - 2i
-2 - 3i
3 + 0i
Some of them are plotted in Argand plane as points and as vectors.
Complex numbers as points :
Complex numbers as vectors :
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
