COMPLEX NUMBERS WITH INEQUALITY PROBLEMS

Complex Numbers with Inequality Problems :

In this section, we will learn, how to solve problems on complex numbers with inequality. 

Complex Numbers with Inequality Problems - Practice Questions

Question 1 :

If | z |= 3, show that 7 ≤ | z + 6 − 8i | ≤ 13.

Solution :

 | z + 6−8i | ≤ | [|z| + |6 − 8i|] |

 ≤ | 3 + √6² + (-8)²|

 ≤ |3 + √(36 + 64)|

 ≤ |3 + √100|

 ≤ |3 + 10|

 ≤ 13

 | z + 6−8i | ≥ |z| - |6 − 8i|

≥ |3 - √(36 + 64)|

≥ |3 - √100|

≥ |3 - 10|

≥  7

7  ≤ | z + 6−8i | ≤ 13

Question 2 :

If |z| = 1, show that 2 ≤ |z² -  3 | ≤ 4

Solution :

|z² -  3 | ≤ ||z²| + |- 3 | |

|z² -  3 | ≤ ||z|² + 3|

|z² -  3 | ≤ |1² + 3| 

|z² -  3 | ≤ 4

|z² -  3 | ≥  ||z²| - | 3||

|z² -  3 | ≥  |1 - 3|

|z² -  3 | ≥ 2

2 ≤ |z² -  3 | ≤ 4

Hence proved.

Question 3 :

If | z - (2/z) | = 2, show that the greatest and least value of | z | are √3 + 1 and √3 − 1 respectively

Solution :

|z - (2/z) | = 2

|(z² - 2)/z | = 2

Question 4 :

If z₁, z₂ and z₃ are three complex numbers such that |z₁| = 1, |z₂|  =  2, |z₃|  =  3 and |z₁ + z₂ + z₃|  =  1, show that |9 z₁ z₂ + 4 z₁ z₃ + z₂ z₃|  =  6

Solution :

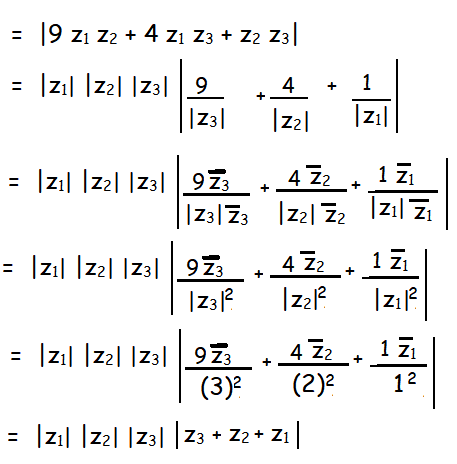
Now applying the given values, we get

  =  1(2)(3) (1)

  =  6

Hence proved.

Question 5 :

If the area of the triangle formed by the vertices z, iz , and z + iz is 50 square units, find the value of z .

Solution :

Length of three sides

z & iz  = √(z-0)² + (0-z)² = |z|√2  =  a

z & z + iz = √(z-z)² + (0-z)² = |z|  =  b 

z & z + iz = √(0-z)² + (z-z)² = |z|  =  c

The sides are |z|√2  , |z|  & |z|

s = (a + b + c)/2

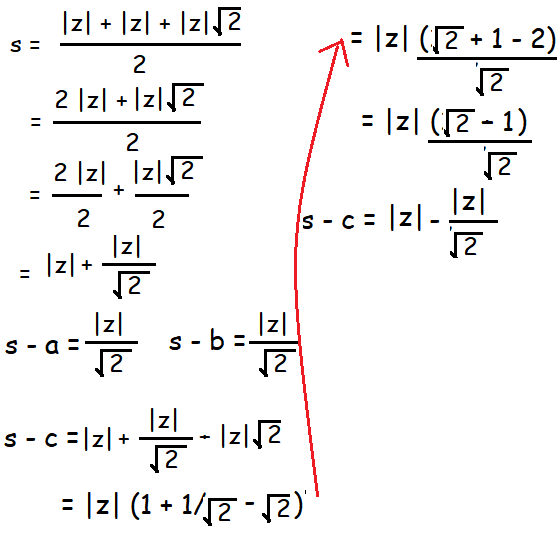
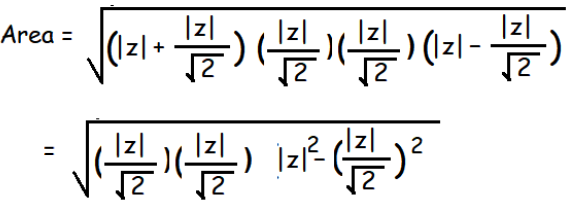
Area of triangle = 50 sq units

|z|²/2  =   50

|z|²  =  100

|z|  =  10

Hence the value of |z|  =  10.

Question 6 :

Show that the equation z³ + 2z bar = 0 has five solutions.

Solution :

z³ + 2z bar = 0

z = x + iy

(x + iy)³ + 2(x - iy)  =  0

x³ + 3x²(iy) + 3 x(iy)² + (iy)³ + 2x - i2y  =  0

x³ + i3x²y - 3 xy² - iy + 2x - i2y  =  0

(x³  - 3 xy² + 2x)  + i(3x²y - y - 2y)  =  0

(x³  - 3 xy² + 2x)  + i(3x²y - 3y)  =  0 + i0

By equating the real and imaginary parts, we get

x³  - 3 xy² + 2x  =  0 ----(1)

3x²y - 3y  =  0 ----(2) 

3y(x² - 1)  =  0

y  =  0, x  =  1, -1

By applying the two different values of x in (1), we get 2 different values of y.

Hence, it has 5 solutions.

After having gone through the stuff given above, we hope that the students would have understood, how to solve complex numbers with inequality problems. 

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.