COMPLETING THE SQUARE WORKSHEET

Problem 1 :

Write x² + 6x + 7 = 0 in the form (x + p)² = q.

Problem 2 :

Solve the following quadratic equation using square root :

x² + 12x + 36 = 49

Problem 3 :

Solve the following quadratic equation by completing the square :

x² - 8x - 9 = 0

Problem 4 :

Write the following quadratic equation in vertex form and graph it :

y = -x² - 2x + 3

What is the maximum or minimum value of the graph of the equation ?

Problem 5 :

Alex plans to create rectangular shaped garden. He has 340 m of fencing available for the garden's perimeter and wants it to have an area of 6000 m². What dimensions should Alex use ?

Problem 6 :

v(t) = -17(t - 26)² + 14750 

The given function v models the value in dollars, of am aircraft t years after its excavation. According to his model, how many years after its excavation was the value of the artifact the greatest ?

Answers

1. Answer :

Write the original equation.

x² + 6x + 7 = 0

Isolate the variable expression.

x² + 6x = -7 -----(1)

Determine the constant needed to complete the square.

Comparing x² + bx and x² + 6x, we get

b = 6

So,

(b/2)² = (6/2)² = 3² = 9

In (1), we have to add 9 to each side.

x² + 6x + 9 = -7 + 9

Write the left side of the equation as a perfect square.

(x + 3)² = 2

Hence, the equation x² + 6x + 7  =  0 can be written as 

(x + 3)² = 2

2. Answer :

Write the original equation.

x² + 12x + 36 = 49

Recognize that the quadratic equation is a perfect square trinomial.

x² + 2(6)(x) + 6² = 49

Factor the perfect square trinomial.

(x + 6)² = 49

Take the square root on each side of the equation.

√(x + 6)² = ± √49

x + 6 = ± 7

x + 6 = -7  or  x + 6 = 7

x = -13  or  x = 1

3. Answer :

Write the original equation.

x² - 8x - 9 = 0

Isolate the variable expression.

x² - 8x = 9 -----(1)

Determine the constant needed to complete the square.

Comparing x² + bx and x² - 8x, we get

b = -8

So,

(b/2)² = (-8/2)² = (-4)² = 16

In (1), we have to add 16 to each side.

x² - 8x + 16 = 9 + 16

x² - 8x + 16 = 25

Write the left side of the equation as a perfect square.

(x - 4)² = 25

Take the square root on each side of the equation.

√(x - 4)² = ± √25

x - 4 = ±5

x - 4 = -5  or  x - 4 = 5

x = -1  or  x = 9

4. Answer :

Write the original equation.

y = -x² - 2x + 3

Factor out the x² coefficient, -1.

y = -1(x² + 2x + 3)

= -1(x² - 2 ⋅ x ⋅ 1 - 3)

= -1(x² - 2 ⋅ x ⋅ 1 - 3)

= -1(x² - 2 ⋅ x ⋅ 1 + 1² - 1² - 3)

= -[(x - 1)² - 1² - 3]

= -[(x - 1)² - 1 - 3]

= -[(x - 1)² - 4]

= -(x - 1)² + 4

Hence, the vertex form of the equation y = -x² - 2x + 3 is

y = -(x - 1)² + 4

Vertex :

The vertex of the parabola is (1, 4).

Graph :

In the given equation y = -x² - 2x + 3, the sign of x² is negative.

So, its graph is a parabola that opens down.

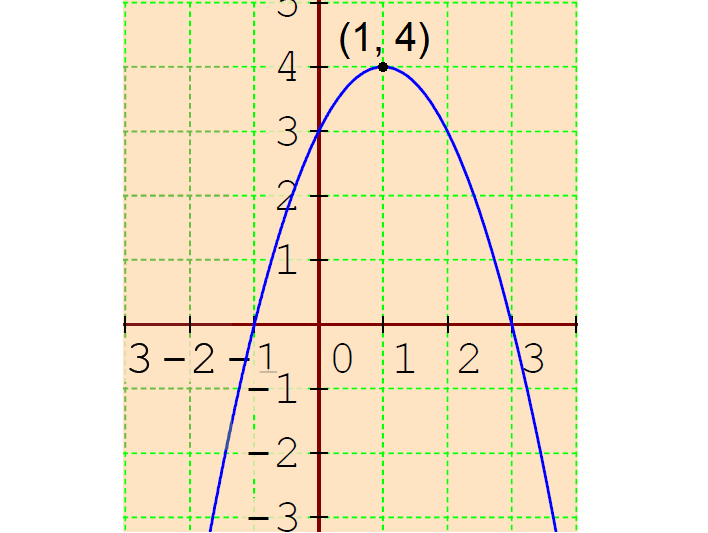
The graph of the given quadratic equation has a maximum of y = 4 at x = 1.

5. Answer :

Let x and y be the length and width of the garden respectively.

Given : Perimeter = 340.

So, we have

2x + 2y = 340

Divide each side by 2.

x + y = 170

Solve for y.

y = 170 - x

Alex wants the area to be 6000 m².

Write this as an equation.

A = xy

6000 = x(170 - x)

6000 = 170x - x²

x² - 170x = -6000 -----(1)

Determine the constant needed to complete the square.

Comparing x² + bx and x² - 170x, we get

b = -170

So,

(b/2)² = (-170/2)² = (-85)² = 7225

In (1), we have to add 7225 to each side.

x² - 170x + 7225 = -6000 + 7225

Write the left side of the equation as a perfect square.

(x - 85)² = 1225

Take the square root on each side of the equation.

√(x - 85)² = ±√1225

x - 85 = ±35

x - 85 = -35  or  x - 85 = 35

x = 50  or  x = 110

When x = 50,

y = 170 - 50

y = 120

When x = 110,

y = 170 - 110

y = 60

In each case, there is 340 m of fencing used.

Likewise, the area is 6000 m².

Hence, Alex should make two sides of the garden 120 m long and the other two sides 50 m long.

6. Answer :

v(t) = -17(t - 26)² + 14750 

The value of the artifact, modeled by v(t) was at its maximum at the vertex of v(t) since v(t) is written in vertex form, it is easy yo see that the vertex is at (26, 44750). Hence the value of artifact was greatest 26 years after its excavation.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.