COMPLEMENT OF A SET

Complement is one of the important operations on sets which can be used to find the difference between the universal set and the given set. 

Let us discuss this operation in detail. 

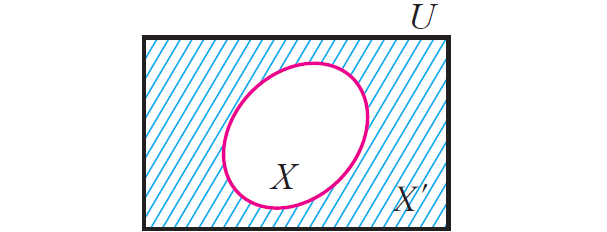
If X ⊆ U, where U is a universal set, then U\X is called the compliment of X with respect to U. If underlying universal set is fixed, then we denote U\X by X' and it is called compliment of X.

X' = U\X or U - X

The difference set set A\B can also be viewed as the compliment of B with respect to A.

Example 1 :

Let U = {1, 2, 3, 4, ......10}, A = {5, 6, 7, 9}, find A'. 

Solution :

A' = U\A

= U - A

= {1, 2, 3, 4, ......10} - {5, 6, 7, 9}

= {1, 2, 3, 4, 8, 10}

Example 2 :

Let U = {1, 2, 3, 4, ......10}. 

A = {1, 3, 4, 5}

B = {3, 4, 5, 6}

C = {1, 2, 3, 5}

Find the following : (A u B)' n (B u C)'.

Solution :

A u B = {1, 3, 4, 5} u {3, 4, 5, 6}

= {1, 3, 4, 5, 6}

(A u B)' = U/(A u B)

= U - (A u B)

= {1, 2, 3, 4, ......10} - {1, 3, 4, 5, 6}

= {2, 7, 8, 9, 10}

B u C = {3, 4, 5, 6} u {1, 2, 3, 5}

= {3, 4, 5, 6, 1, 2}

(B u C)' = U/(B u C)

= U - (B u C)

= {1, 2, 3, 4, ......10} - {3, 4, 5, 6, 1, 2}

= {7, 8, 9, 10}

(A u B)' n (B u C)' = {2, 7, 8, 9, 10} u {7, 8, 9, 10}

= {7, 8, 9, 10}

Related Pages

1. Union of sets

2. Intersection of sets

3. Set difference

4. Symmetric difference of two sets

5. Disjoint sets

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.