COMPARING RATIOS WORD PROBLEMS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Anna’s recipe for lemonade calls for 2 cups of lemonade concentrate and 3 cups of water. Bailey’s recipe calls for 3 cups of lemonade concentrate and 5 cups of water. Whose recipe makes stronger lemonade ? How do you know ?
Problem 2 :
There are two alloys A and B, both are made up of gold and copper. The ratio between gold and copper in each alloy is given below.
Alloy A (G : C)----> 2 1/3 : 3 1/3
Alloy B (G : C) ----> 3.6 : 4.8
In which alloy do we have more gold ?
Problem 3 :
A fruit and nut bar recipe calls for 4 cups of chopped nuts and 6 cups of dried fruit. Tonya increased the recipe. She used 6 cups of chopped nuts and 9 cups of dried fruit. Did Tonya use the correct ratio of nuts to fruit ?
Problem 4 :
In the science club, there are 2 sixth graders for every 3 seventh graders. At this year’s science fair, there were 7 projects by sixth graders for every 12 projects by seventh graders. Is the ratio of sixth graders to seventh graders in the science club equivalent to the ratio of science fair projects by sixth graders to projects by seventh graders ?
1. Answer :
Anna’s recipe :
2 cups of lemonade and 3 cups of water.
So, the ratio is 2 : 3.
Let us write equivalent ratios to the ratio 2 : 3.

Bailey’s recipe :
3 cups of lemonade and 5 cups of water.
So, the ratio is 3 : 5.
Let us write equivalent ratios to the ratio 3 : 5.

Find two columns, one in each table, in which the amount of water is the same. Circle those two columns.
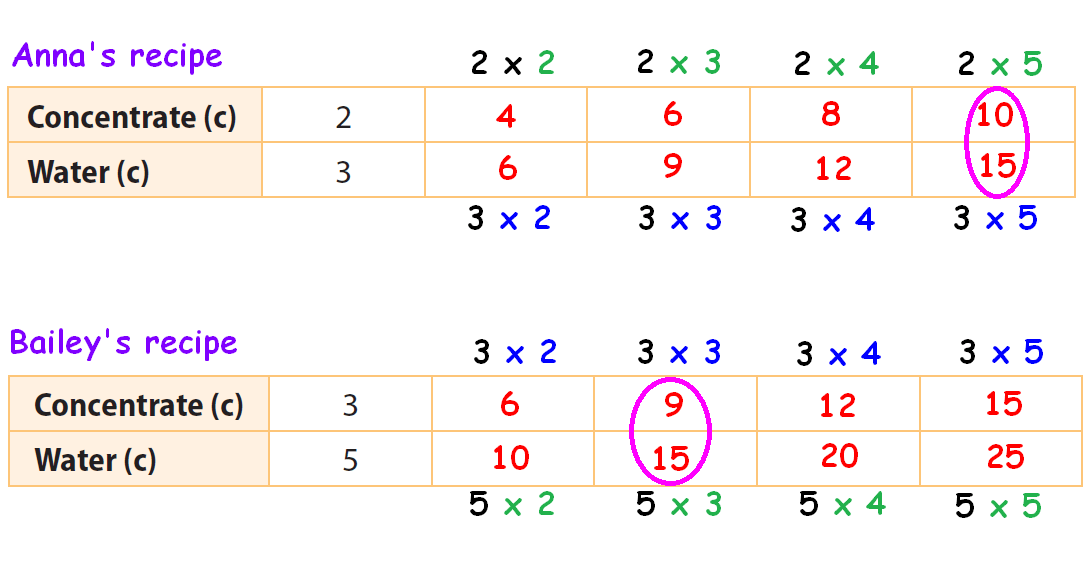
From the circled columns, we get two ratios.
They are,
10 : 15 and 9 : 15
In these two ratios, the second quantity (water) is same.
So, we have to compare the first quantity (Lemonade).
The first quantity (10) in the first ratio is more than the first quantity (9) in the second ratio.
When the amount of water is same (15) in both recipes, Anna's recipe has more quantity of lemonade concentrate.
Therefore, Anna's recipe has stronger lemonade.
2. Answer :
To know the alloy in which we have more gold, we have to compare the given two ratios.
To compare two ratios, both the terms of the ratio must be integers.
Let us convert the terms of the first ratio into integers.
2⅓ : 3⅓ = 7/3 : 10/3
2⅓ : 3⅓ = 7 : 10 ----> multiplied by 3
Let us write equivalent ratios to the ratio 7 : 10.
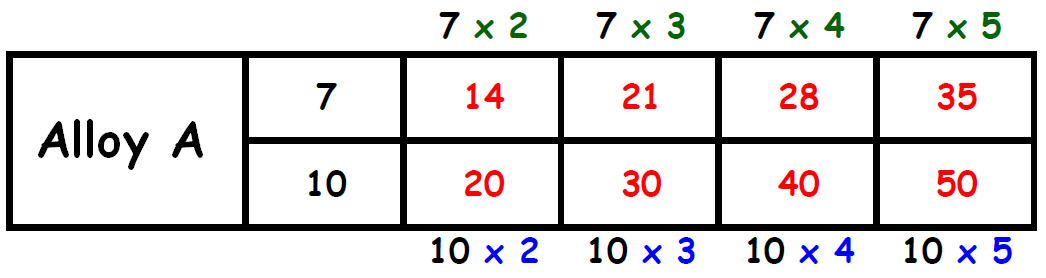
Let us convert the terms of the second ratio into integers.
3.6 : 4.8 = 36 : 48 ------> multiplied by 10
3.6 : 4.8 = 3 : 4 ------> divided by 12
Let us write equivalent ratios to the ratio 3 : 4
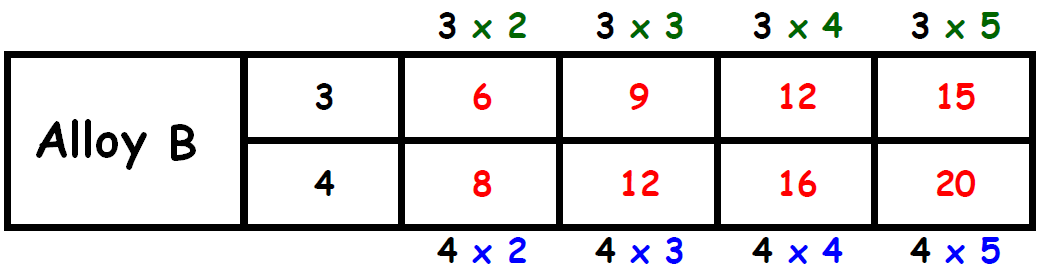
Find two columns, one in each table, in which the the second term is same. Circle those two columns.
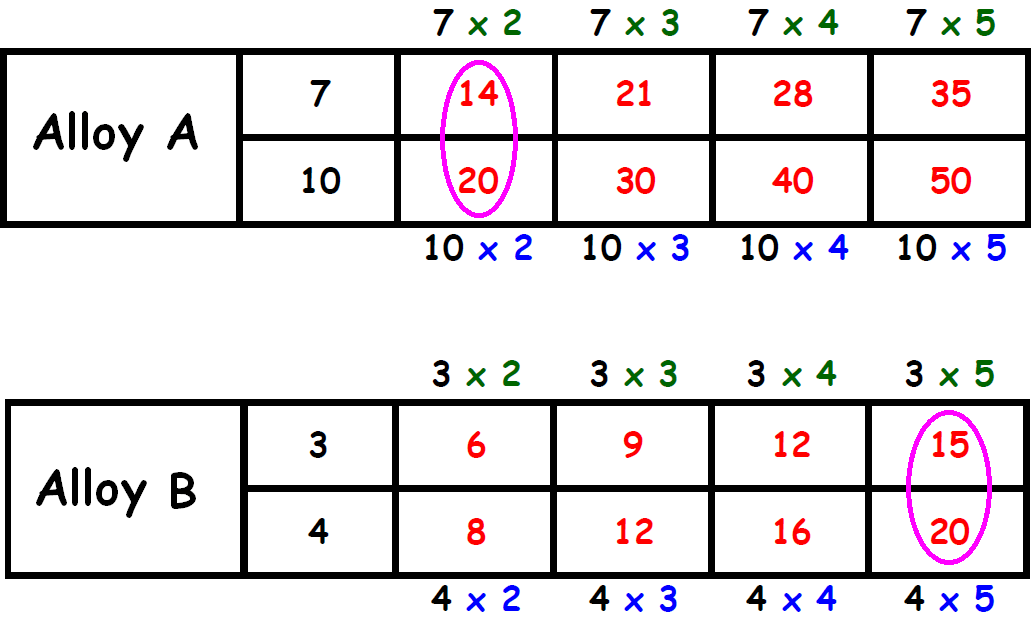
From the circled columns, we get two ratios.
They are,
14 : 20 and 15 : 20
In these two ratios, the second quantity (copper) is same.
So, we have to compare the first quantity (gold).
The first quantity (15) in the second ratio is more than the first quantity (14) in the first ratio.
When the quantity of copper is same (20) in both the alloys, Alloy A has more quantity of gold.
Therefore, we have more gold in alloy A.
3. Answer :
Step 1 :
Find the ratio of nuts to fruit in the recipe.
That is,
4/6
(4 cups of nuts to 6 cups of fruit)
Step 2 :
Find the ratio of nuts to fruit that Tonya used.
That is,
6/9
(6 cups of nuts to 9 cups of fruit)
Step 3 :
Find equivalent ratios that have the same second term.
That is,
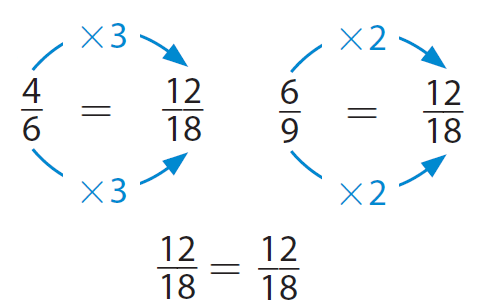
(18 is a multiple of 6 and 9, so, we find equivalent ratios with 18 in the second term)
The ratios 4/6 and 6/9 are equivalent.
Therefore, Tonya used the same ratio of nuts to fruit that was given in the recipe.
4. Answer :
Step 1 :
Find the ratio of sixth grader and seventh graders.
That is,
2/3
(2 sixth graders to 3 seventh graders)
Step 2 :
Find the ratio of science fair projects by sixth graders to projects by seventh graders
That is,
7/12
(7 projects by sixth graders to 12 projects by sixth graders)
Step 3 :
Find equivalent ratios that have the same second term.
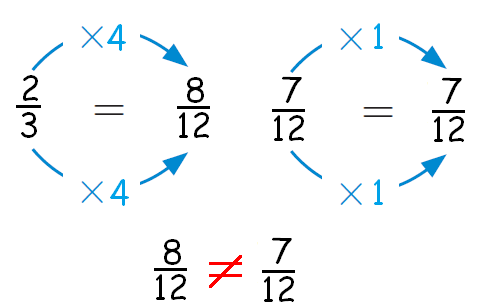
(12 is a multiple of 3 and 12, so, we find equivalent ratios with 12 in the second term)
But 2/3 and 7/12 are not equivalent.
Because, the equivalent of ratio of 2/3 and equivalent ratio of 7/12 are not equal.
That is,
8/12 ≠ 7/12
Therefore, the ratio of sixth graders to seventh graders in the science club is not equivalent to the ratio of science fair projects by sixth graders to projects by seventh graders
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
SAT Math Problems and Solutions
Feb 14, 26 06:05 AM
SAT Math Problems and Solutions -
SAT Math Practice Questions with Answers
Feb 14, 26 05:47 AM
SAT Math Practice Questions with Answers -
SAT Math Practice Test with Answers
Feb 14, 26 02:30 AM
SAT Math Practice Test with Answers