COMPARING PROPORTIONAL AND NONPROPORTIONAL SITUATIONS

Example 1 :

A laser tag league has the choice of two arenas for a tournament. In both cases, x is the number of hours and y is the total charge. Compare and contrast these two situations.

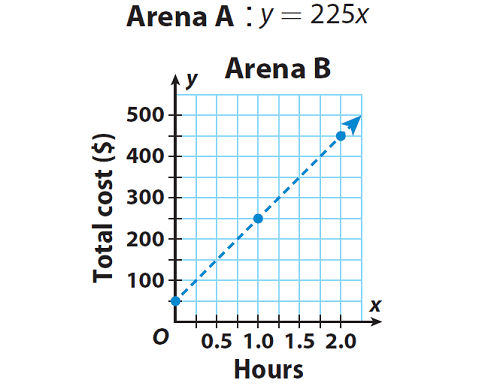
Solution :

Arena A :

Arena A’s equation has the form y = mx + b, where b = 0. So, Arena A’s charges are a proportional relationship. The hourly rate, $225, is greater than Arena B’s, but there is no additional fee.

Arena A :

Arena B’s graph is a line that does not include the origin. So, Arena B’s charges are a non-proportional relationship. Arena B has a $50 initial fee but its hourly rate, $200, is lower.

Example 2 :

Jessika is remodeling and has the choice of two painters. In both cases, x is the number of hours and y is the total charge. Compare and contrast these two situations.

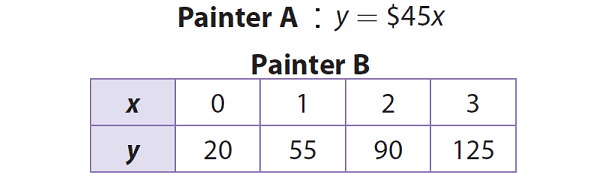
Solution :

Painter A :

Painter A’s equation has the form y = mx + b, where b = 0. So, Painter A’ s charges are proportional. The hourly rate, $45, is greater than Painter B’s, but there is no additional fee.

Painter B :

Painter B’s table is a nonproportional relationship because the ratio of y to x is not constant. Because the table contains the ordered pair (0, 20), Painter B charges an initial fee of $20, but the hourly rate, $35, is less than Painter A’s.

Example 3 :

Compare and contrast the following two situations.

Solution :

Test-Prep Center B :

Test-Prep Center A is cheaper for greater than 20 hours;

Test-Prep Center B :

Test-Prep Center B is cheaper for less than 20 hours.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.