COMPARING EXPRESSIONS USING MODELS

Algebraic expressions are equivalent if they are equal for all values of the variable.

For example,

x + 2 and x + 1 + 1 are equivalent

Because, "x + 2" and "x + 1 + 1" are equal for all real values.

We can use models to compare expressions. 

Let us see how models can be used to compare expressions. 

Examples

Example 1 : 

Katriana and Andrew started the day with the same amount of money. Katriana spent 5 dollars on lunch. Andrew spent 3 dollars on lunch and 2 dollars on a snack after school. Do Katriana and Andrew have the same amount of money left ?

Solution :

Let x be the money that Katriana and Andrew had at the beginning. 

Step 1 :

Write an algebraic expression to represent the money Katriana has left.

x - 5

Represent the expression with a model.

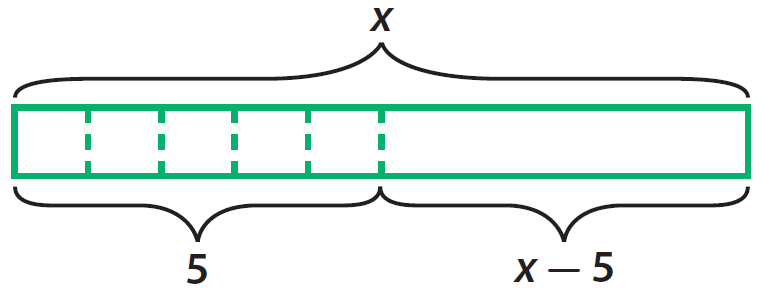
Step 2 :

Write an algebraic expression to represent the money Andrew has left.

x - 3 - 2

Represent the expression with a model.

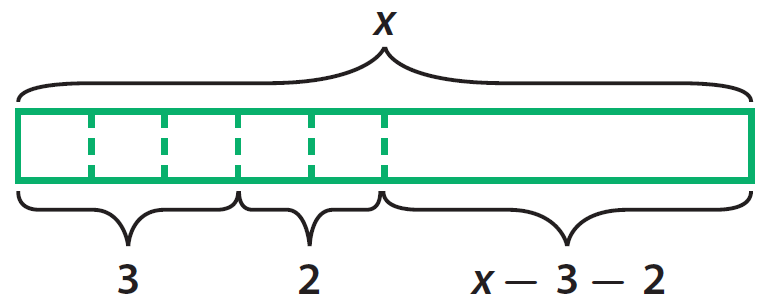
Step 3 :

Compare the models.

The models are equivalent, so the expressions are equivalent.

Andrew and Katriana have the same amount of money left.

Example 2 : 

On a math quiz, Tina scored 3 points more than Julia. Juan scored 2 points more than Julia and earned 2 points in extra credit. Write an expression and draw a bar model to represent Tina’s score and Juan’s score. Did Tina and Juan make the same grade on the quiz ? Explain.

Solution :

Let y be the points scored by Julia. 

Step 1 :

Write an algebraic expression to represent the points scored by Tina.

y + 3

Represent the expression with a model.

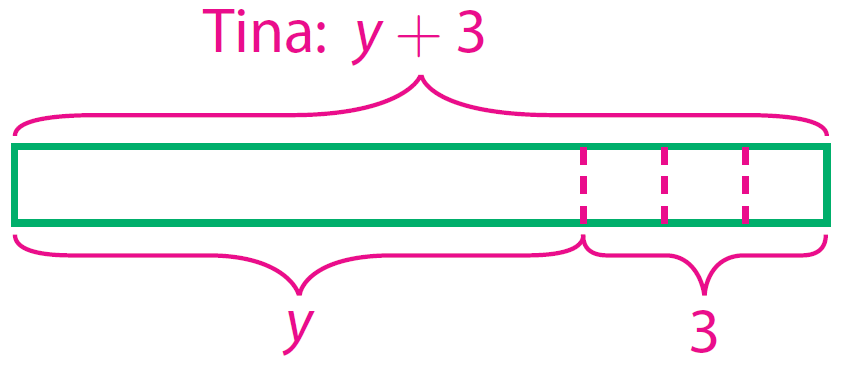
Step 2 :

Write an algebraic expression to represent the points scored by Juan.

y + 2 + 2

Represent the expression with a model.

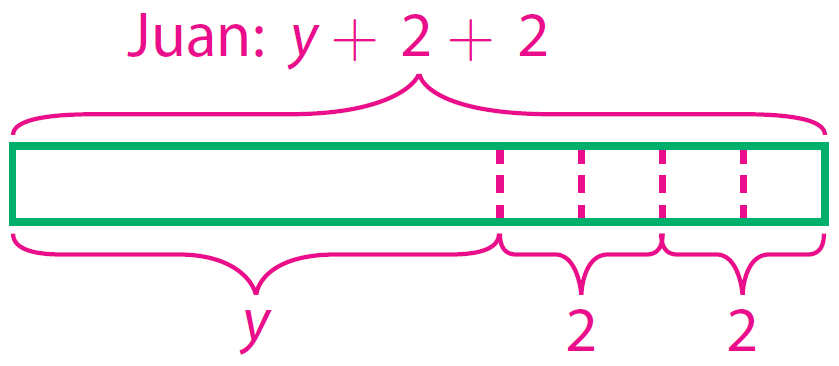
Step 3 :

Compare the models.

The models are not equivalent, so the expressions are not equivalent.

So, Tina and Juan did not make the same grade on the quiz.

Example 3 : 

At 6 p.m., the temperature in Phoenix, AZ, t, is the same as the temperature in Tucson, AZ. By 9 p.m., the temperature in Phoenix has dropped 2 degrees and in Tucson it has dropped 4 degrees. By 11 p.m., the temperature in Phoenix has dropped another 3 degrees. At 11 pm, are  the temperatures in the two cities equivalent ? Explain

Solution :

Let t be the temperature of the two cities at 6 p.m 

Step 1 :

Write an algebraic expression to represent temperature of the city Phoenix at 11 p.m.

y - 2 - 3

Represent the expression with a model.

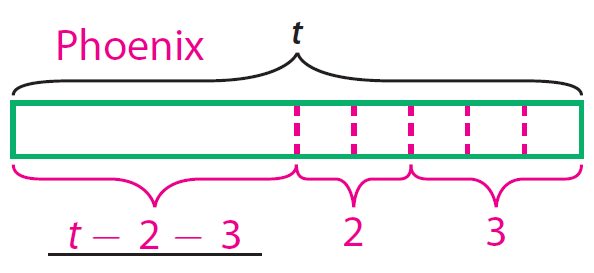
Step 2 :

Write an algebraic expression to represent temperature of the city Tucson at 11 p.m.

y - 4

Represent the expression with a model.

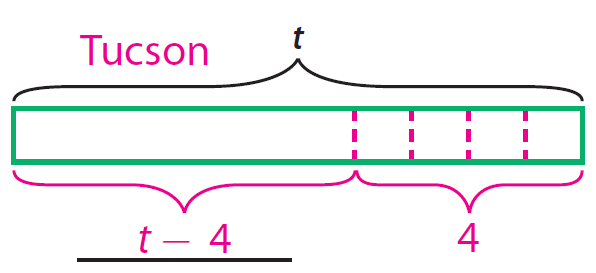
Step 3 :

Compare the models.

The models are not equivalent, so the expressions are not equivalent.

Hence, At 11 pm, the temperatures in the two cities are not equivalent

The models show that the temperature in Phoenix is 1 degree less than the temperature in Tucson at 11 p.m. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.