COMPARING AND ORDERING RATIONAL NUMBERS

Example 1 :

Find which of the given two fractions is greater :

6/19 and 16/19

Solution :

Since the denominators of those fractions are same, compare the numerators.

6 < 16

So, 16/19 is greater than 6/19.

Example 2 :

Find which fraction is greater :

1/2 and 3/5

Solution :

For the given two fractions, the denominators are different. Make the denominator of each fraction same using least common multiplication of the denominators.

Lest common multiple of (2, 5) is 10.

1/2 = (1 x 5)/(2 x 5) = 5/10

3/5 = (3 x 2)/(5 x 2) = 6/10

Since the denominators of the two fractions 5/10 and 6/10 are same, compare the numerators.

5 < 10

5/10 < 6/10

Substitute the corresponding original fractions.

1/2 < 3/5

So, 3/5 is greater than 1/2.

Example 3 :

Compare 1.031 and 0.256.

Solution :

To compare the given decimal numbers, we have to write them in a table as given below.

In the above table, compare the numbers in the first column (units).

We have 1 in 1.0231 and 0 in 0.256.

Because 1 is greater than 0, we have

1.031 is greater than 0.256

Example 4 :

Compare 0.231 and 0.228.

Solution :

To compare the given decimal numbers, we have to write them in a table as given below.

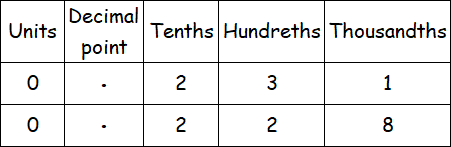
In the above table, compare the numbers in the first column (units).

In the first column, we have have 0 in both the decimal numbers 0.231 and 0.228.

So, we have to compare the numbers in the third column (Tenths).

In the third column (Tenths), we have the same number 2 in both the decimal numbers.

So, we have to compare the numbers in fourth column (Hundredths).

In the fourth column (Hundredths), we have 3 in 0.231 and 2 in 0.228.

Since 3 is greater than 2, we have

0.231 is greater than 0.228

Example 5 :

Order the fractions from least to greatest 3/4, 2/5, 1/8.

Solution :

For the given fractions, the denominators are different. Make the denominator of each fraction same using least common multiplication of the denominators.

Lest common multiple of (2, 5, 8) is 40.

3/4 = (3 x 10)/(4 x 10) = 30/40

2/5 = (2 x 8)/(5 x 8) = 16/40

1/8 = (1 x 5)/(8 x 5) = 5/40

Since the denominators of the fractions 3/40, 16/40 and 5/40 are same, compare and order the numerators from least to greatest.

5/40 < 16/40 < 30/40

Substitute the corresponding original fractions.

1/8 < 2/5 < 3/4

Example 6 :

Order the decimal numbers 1.023, 1.101 and 0.985 from least to greatest.

Solution :

To order the given decimal numbers, first we have to write them in a table as given below.

To get the least one, compare the numbers in the first column (units).

We get 0 in 0.985. This is the least among the given three decimal numbers.

To get the next least number, let us compare 1.023 and 1.101.

In both the decimals, we find 1 in the first column (units).

Now, we have to compare the third column (Tenths). There we get 0 in 1.023 and 1 in 1.101.

Since 0 is less than 1, the next least decimal is 1.023.

Therefore, the order of the given decimals from least to greatest is

0.985, 1.023, 1.101

Example 7 :

Five friends completed a triathlon that included a 3-mile run, a 12-mile bike ride, and a 1/2 -mile swim. To compare their running times they created a table that shows the difference between each person’s time and the average time, with negative numbers representing times less than the average.

Use a number line to order the numbers from greatest to least.

Solution :

Step 1 :

Write the fractions as equivalent decimals.

1/2 = 0.5 and -1 1/4 = -1.25

Step 2 :

Use the number line to write the decimals in order.

From the above number line, we have the numbers in order from greatest to least are

1.95, 1.4, 1/2, -1 1/4, -2.0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.