COMPARING AND ORDERING INTEGERS

We use number line to compare and order integers.

That is,  if we want to compare two integers, first we have to locate the integers on the number line and mark them.

The integer which comes to the right of the other integer is greater. The integer which comes to the left of the other integer is smaller.

To order the integers, we have to locate the given integers on the number line and mark them. Then, write the integers from left to right to list them in order from least to greatest.

Comparing Integers

Example 1 :

Compare the integers -4 and 4.

Solution :

Let us locate the two integers -4 and 4 on a number line and mark them.

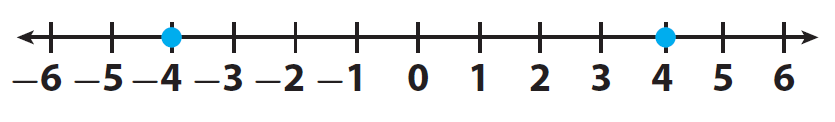
Here, the positive integer 4 comes to the right of -4.

Therefore 4 is greater than -4.

And -4 comes to the left of 4.

Therefore -4 is smaller than 4.

Example 2 :

Compare the integers -1 and 1.

Solution :

Let us locate the two integers -1 and 1 on a number line and mark them.

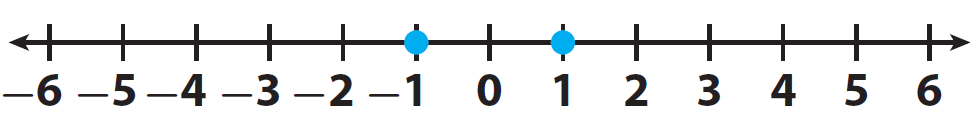
Here, the positive integer 1 comes to the right of -1.

Therefore 1 is greater than -1.

And -1 comes to the left of 1.

Therefore -1 is smaller than 1.

Ordering Integers

Question :

Order the integers -2, -5, 4, 0, -3, -1, 3 from least to greatest.

Answer :

Let us locate the integers -2, -5, 4, 0, -3, -1, 3 on a number line and mark them.

From the above number line, write the integers from left to right to list them in order from least to greatest.

Thus, we get

-5, -3, -2, -1, 0, 3, 4

Real World Problems

Problem 1 :

In 2010, Sacramento, California, received 23 inches in annual precipitation. In 2011, the city received 17 inches in annual precipitation. In which year was there more precipitation?

Solution :

Locate the two integers 23 and 17 on a number line and mark them.

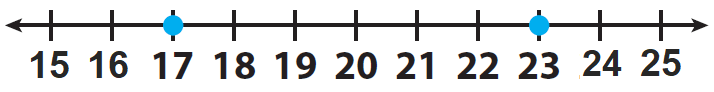
23 is to the right of 17 on the number line.

This means that 23 is greater than 17.

We can write the above situation in terms of inequality as 23 > 17.

17 is to the left of 23 on the number line.

This means that 17 is less than 23.

We can write the above situation in terms of inequality as 17 < 23.

There was more precipitation in 2010.

Problem 2 :

John recorded the following golf scores during his first week at a golf academy. Negative numbers represent scores below par, a standard score. In golf, a lower score beats a higher score.

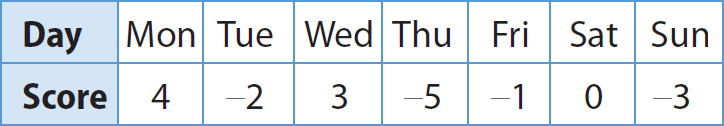
Graph John’s scores on the number line, and then list the numbers in order from least to greatest.

Solution :

Step 1 :

Graph the scores on the number line.

Step 2 :

Read from left to right to list the scores in order from least to greatest.

The scores listed from least to greatest are

–5, –3, –2, –1, 0, 3, 4.

Problem 3 :

a) Arrange in descending order 5, -4, 0, 1, -1, -3, -6

b) Find the difference between the largest and smallest values.

c) Find the sum of numbers in a)

Solution :

Descending order means arranging the values from greatest to least.

Positive numbers are greater than negative numbers.

5, 1, 0, -1, -3, -4, -6

b) By observing the arrangements, we know that

greater number = 5

smaller number = -6

Difference = 5 - (-6)

= 5 + 6

= 11

So, the required difference is 11.

c) Sum of the numbers = 5 + 1 + 0 -1 -3 - 4 - 6

= 6 - 14

= -8

So, the required sum is -8.

Problem 4 :

Draw the number lines to show the following sets of numbers. Use different number line for each set.

a)  -9, 2, 5

b)  2, 6, 8, -3, -4

c)  9, -4, -9, 1, 6, -6

d)  -3, 2, 5, -5, 0, -1

Solution :

a)  -9, 2, 5

After arranging the numbers from least to greatest, we can put it in the number line easily.

b)  2, 6, 8, -3, -4

Arranging from least to greatest,

-4, -3, 2, 6, 8

c)  9, -4, -9, 1, 6, -6

Arranging from least to gratest,

-9, -6, -4, 1, 6, 9

d)  -3, 2, 5, -5, 0, -1

Arranging the numbers from least to greatest,

-5, -3, -1, 0, 2, 5

Problem 5 :

Arrange in descending order

0, -5, 8, -7, -2 and 6

Solution :

Descending means arrangement should be done from greatest to least.

8, 6, 0, -2, -5, -7

Problem 6 :

Arrange in ascending order.

0, -10, 8, 7, -7 and -2

Solution :

Descending means arrangement should be done from least to greatest.

-10, -7, -2, 0, 7 and 8.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.