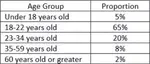
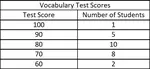
COMPARING AND ORDERING FRACTIONS

Find which fraction is greater :

Example 1 :

6/19 and 16/19

Solution :

In the fractions 6/19 and 16/19, the denominator is same. So, the fraction which has greater numerator will greater in value.

16/9 > 6/19

16/19 is greater than 6/19

Example 2 :

1/2 and 3/5

Solution :

In the fractions 1/2 and 3/5, the denominators are different.

Make the denominators same using least common multiple.

Least common multiple of (2, 5) = 10.

1/2 = (1 ⋅ 5)/(2 ⋅ 5) = 5/10

3/5 = (3 ⋅ 2)/(5 ⋅ 2) = 15/10

Compare the numerators of like fractions 5/10 and 15/10.

15/10 > 5/10

Substitute the corresponding original fractions.

3/5 > 1/2

3/5 is greater than 1/2

Example 3 :

7/12 and 11/18

Solution :

In the fractions 7/12 and 11/18, the denominators are different.

Make the denominators same using least common multiple.

Least common multiple of (12, 18) = 36.

7/12 = (7 ⋅ 3)/(12 ⋅ 3) = 21/36

11/18 = (11 ⋅ 2)/(18 ⋅ 2) = 22/36

Compare the numerators of like fractions 21/36 and 22/36.

22/36 > 21/36

Substitute the corresponding original fractions.

11/18 > 7/12

11/18 is greater than 7/12

Order the fractions from least to greatest :

Example 4 :

5/19, 7/19, 2/19, 3/19

Solution :

In all the given fractions, the denominator is same.

Compare the numerators and order them from least to greatest.

2/19, 3/19, 5/19, 7/19

Example 5 :

3/4, 2/5, 1/8

Solution :

In the given fractions, the denominators are different.

Make the denominator same using least common multiple and order them from least to greatest.

Least common multiple of (4, 5, 8) = 40.

3/4 = (3 ⋅ 10)/(4 ⋅ 10) = 30/40

2/5 = (2 ⋅ 8)/(5 ⋅ 8) = 16/40

1/8 = (1 ⋅ 5)/(8 ⋅ 5) = 5/40

Compare the numerators of like fractions above and order them from least to greatest.

5/40, 16/40, 30/40

Substitute the corresponding original fractions.

1/8, 2/5, 3/4

Example 6 :

5/6, 1/4, 3/8, 7/12

Solution :

In the given fractions, the denominators are different. 

Make the denominator same using least common multiple and order them from least to greatest.

Least common multiple of (6, 4, 8, 12) = 24.

5/6 = (5 ⋅ 4)/(6 ⋅ 4) = 20/24

1/4 = (1 ⋅ 6)/(4 ⋅ 6) = 6/24

3/8 = (3 ⋅ 3)/(8 ⋅ 3) = 9/24

7/12 = (7 ⋅ 2)/(12 ⋅ 2) = 14/24

Compare the numerators of like fractions above and order them from least to greatest.

6/24, 9/24, 14/24, 20/24

Substitute the corresponding original fractions.

1/4, 3/8, 7/12, 5/6

Order the fractions from greatest to least :

Example 7 :

3/4, 2/5, 5/8, 1/2

Solution :

In the given fractions, the denominators are different.

Make the denominator same using least common multiple and order them from greatest to least.

Least common multiple of (4, 5, 8, 2) = 40.

3/4 = (3 ⋅ 10)/(4 ⋅ 10) = 30/40

2/5 = (2 ⋅ 8)/(5 ⋅ 8) = 16/40

5/8 = (5 ⋅ 5)/(8 ⋅ 5) = 25/40

1/2 = (1 ⋅ 20)/(2 ⋅ 20) = 20/40

Compare the numerators of like fractions above and order them from greatest to least.

30/40, 25/40, 20/40, 16/40

Substitute the corresponding original fractions.

3/4, 5/8, 1/2, 2/5

Example 8 :

1/6, 1/3, 3/14, 2/7

Solution :

Make the denominator same using least common multiple and order them from greatest to least.

Least common multiple of (6, 3, 14, 7) = 42.

1/6 = (1 ⋅ 7)/(6 ⋅ 7) = 7/42

1/3 = (1 ⋅ 14)/(3 ⋅ 14) = 14/42

3/14 = (3 ⋅ 3)/(14 ⋅ 3) = 9/42

2/7 = (2 ⋅ 6)/(7 ⋅ 6) = 12/42

Compare the numerators of like fractions above and order them from greatest to least.

14/42, 12/42, 9/42, 7/42

Substitute the corresponding original fractions.

1/3, 2/7, 3/14, 1/6

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.