COMPARING AND ORDERING DECIMALS

In Math, sometimes we people find it difficult to do problems with decimals like comparing and ordering of decimal numbers.

Actually it is not difficult to do problems with decimals, once we understand the stuff.

Now, let us see how to compare two decimals.

Comparing Decimals

Example 1 :

Compare 1.031 and 0.256.

Solution :

To compare the given decimal numbers, we have to write them in a table as given below.

In the above table, compare the numbers in the first column (units).

We have 1 in 1.0231 and 0 in 0.256.

Since 1 is greater than 0, we have

1.031 is greater than 0.256

Example 2 :

Compare 0.231 and 0.228.

Solution :

To compare the given decimal numbers, we have to write them in a table as given below.

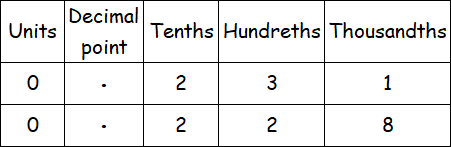
In the above table, compare the numbers in the first column (units).

In the first column, we have have 0 in both the decimal numbers 0.231 and 0.228.

So, we have to compare the numbers in the third column (Tenths).

In the third column (Tenths), we have the same number 2 in both the decimal numbers.

So, we have to compare the numbers in fourth column (Hundredths).

In the fourth column (Hundredths), we have 3 in 0.231 and 2 in 0.228.

Since 3 is greater than 2, we have

0.231 is greater than 0.228

Ordering Decimals

Example 3 :

Order the decimal numbers 1.023, 1.101 and 0.985 from least to greatest.

Solution :

To order the given decimal numbers, first we have to write them in a table as given below.

To get the least one , compare the numbers in the first column (units).

We get 0 in 0.985. This is the least among the given three decimal numbers.

To get the next least number, let us compare 1.023 and 1.101.

In both the decimals, we find 1 in the first column (units).

Now, we have to compare the third column (Tenths). There we get 0 in 1.023 and 1 in 1.101.

Since 0 is less than 1, the next least decimal is 1.023.

Therefore, the order of the given decimals from least to greatest is

0.985, 1.023, 1.101

Example 4 :

Order the decimal numbers 0.098, 0.123 and 0.985 from least to greatest.

Solution :

To order the given decimal numbers, first we have to write them in a table as given below.

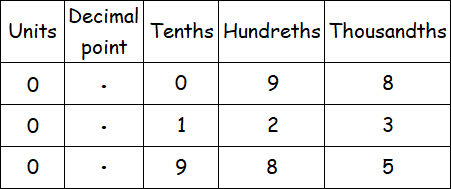
To get the least one , compare the numbers in the first column (Units).

We get 0 in all the three decimal numbers in the first column.

So, let us move to the third column (Tenths) and compare the numbers.

In third column, we get 0 in 0.098.

Therefore, 0.098 is the least among the given decimal numbers.

In the same third column, we get 1 in 0.123.

This is the next least decimal number.

Therefore, the order of the given decimals from least to greatest is

0.098, 0.123, 0.985

Note :

In the third column also, if you get the same number in all the three decimal numbers, compare the numbers in the fourth column (Hundredths column) and so on.

Example 5 :

Write in order from smallest to largest 8.66, 8.6, 8.606

Solution :

To compare decimals, we can convert the decimals as like decimals then comparision can be done simply. Since we have three digits after the decimal maximum. 

8.660, 8.600, 8.606

8.600, 8.606, 8.660.

So, the correct order from least to greatest is 

8.6, 8.606, 8.66

Example 6 :

Write in ascending order.

a)  1.36, 1.3, 1.036

b)  8.76, 8.67, 8.6

c) 0.5, 0.495, 0.052

Solution :

a)  1.36, 1.3, 1.036

Converting into like decimals :

1.360, 1.300, 1.036

Arranging from least to greatest, 

1.036, 1.300, 1.360

So, ascending order is 

1.036, 1.3, 1.36

b)  8.76, 8.67, 8.6

Converting into like decimals :

8.76, 8.67, 8.60

Arranging from least to greatest, 

8.60, 8.67, 8.76

So, ascending order is 

8.6, 8.67, 8.76

c) 0.5, 0.495, 0.052

Converting into like decimals :

0.500, 0.495, 0.052

Arranging from least to greatest, 

0.052, 0.495, 0.500

So, ascending order is 

0.052, 0.495, 0.5

Example 7 :

Patricia's best four times for a 100 m sprint are 16.98 seconds, 16.91 seconds, 17.91 seconds and 17.1 seconds. Place the times in order from fastest to slowest.

The given seconds are,

16.98, 16.91, 17.91, 17.1

Converting into like decimals :

16.98, 16.91, 17.91, 17.10

Arragning from least to greatest :

16.91, 16.98, 17.10, 17.91

Example 8 :

On Monday The Euro could be exchanged for 1.3537 US dollars. For the rest of the week, the exchange figures are :

Tuesday 1.3571, Wednesday 1.3602, Thursday 1.3519 and Friday 1.3578

a) Place these exchange rates in order from highest to lowest.

b) On which day was the exchange rate,

i) highest   ii) lowest

Solution :

a) Givne that, 

Tuesday 1.3571, Wednesday 1.3602, Thursday 1.3519 and Friday 1.3578

Arranging from least to greatest,

1.3519, 1.3571, 1.3578, 1.3602

b) The highest exchange rate is on Wednesday

The lowest exchange rate is on Thursday.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.