COMPARE PERCENTS TO FRACTIONS AND DECIMALS

Comparing Percents To Fractions - Steps

Step 1 :

Write the given percentage as fraction.

For example, if it is 15% then write it as 15/100.

Step 2 :

Convert the denominator of the given fraction as 100 using multiplication. 

So that, on either sides we will have fractions with same denominators.

Step 3 :

Now we can easily compare the numerators and decide which number is greater and which number is smaller.

Note : 

If it is not possible to convert the denominator of the given fraction into 100 using multiplication, better convert both percent and fraction into decimal and compare. 

Comparing Percents to Decimals - Steps

Step 1 :

Write the given percentage as fraction. That is, if we have 15% then write it as 15/100.

Step 2 :

Multiply and divide the given decimal by 100.

So that, on either sides we will have fractions with same denominators.

Step 3 :

Now we can easily compare the numerators and decide which number is greater and which number is smaller.

Examples

Example 1 :

Which of the following signs makes the statement true ?

< ,  > ,  =

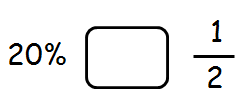
Solution :

We can write 20% as shown below. 

20 / 100 -----(1)

Multiply both numerator and denominator of the fraction 1/2 by 50 as shown below.

(1 / 2) ⋅ (50 / 50)  =  50 / 100 -----(2)

In fractions (1) and (2), the denominators are same.

Now, we can compare the numerators.

20 is lesser than 50

So, 20% is lesser than 1/2.

Example 2 :

Which sign makes the statement true?

< ,  > ,  =

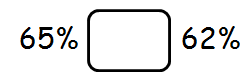
Solution :

Here, both the quantities are percents.

So, we can easily compare them. 

65% is greater than 62%

Example 3 :

Which sign makes the statement true?

< ,  > ,  =

Solution :

We can write 7% as shown below. 

7 / 100 -----(1)

Multiply both numerator and the denominator of the fraction 1/4 by 25 as shown below.

(1 / 4) ⋅ (25 / 25)  =  25 / 100 -----(2)

In fractions (1) and (2), the denominators are same.

Now, we can compare the numerators.

7 is lesser than 25 

So, 7% is lesser than 1/4.

Example 4 :

Which sign makes the statement true?

< ,  > ,  =

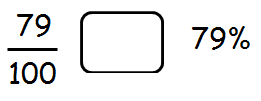
Solution :

In the fraction 79/100, already the denominator is 100.

So, we have nothing more to do in the fraction 79/100.

79 / 100 -----(1)

We can write 79% as shown below. 

79 / 100 -----(2)

In fractions (1) and (2), both the numerators and denominators are same.

So, 79/100 and 79% are equal.

Example 5 :

Which sign makes the statement true?

< ,  > ,  =

Solution :

We can write 3% as shown below. 

3 / 100 -----(1)

Multiply and divide the decimal 0.07 by 100 as shown below. 

0.07 ⋅ (100 / 100)  =  7 / 100 -----(2)

In fractions (1) and (2), the denominators are same.

Now, we can compare the numerators.

3 is lesser than 7

So, 3% is lesser than 0.07

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

If you have any feedback about our math content, please mail us : 

v4formath@gmail.com

We always appreciate your feedback. 

You can also visit the following web pages on different stuff in math. 

WORD PROBLEMS

HCF and LCM  word problems

Word problems on simple equations 

Word problems on linear equations 

Word problems on quadratic equations

Algebra word problems

Word problems on trains

Area and perimeter word problems

Word problems on direct variation and inverse variation 

Word problems on unit price

Word problems on unit rate 

Word problems on comparing rates

Converting customary units word problems 

Converting metric units word problems

Word problems on simple interest

Word problems on compound interest

Word problems on types of angles 

Complementary and supplementary angles word problems

Double facts word problems

Trigonometry word problems

Percentage word problems 

Profit and loss word problems 

Markup and markdown word problems 

Decimal word problems

Word problems on fractions

Word problems on mixed fractrions

One step equation word problems

Linear inequalities word problems

Ratio and proportion word problems

Time and work word problems

Word problems on sets and venn diagrams

Word problems on ages

Pythagorean theorem word problems

Percent of a number word problems

Word problems on constant speed

Word problems on average speed 

Word problems on sum of the angles of a triangle is 180 degree

OTHER TOPICS 

Profit and loss shortcuts

Percentage shortcuts

Times table shortcuts

Time, speed and distance shortcuts

Ratio and proportion shortcuts

Domain and range of rational functions

Domain and range of rational functions with holes

Graphing rational functions

Graphing rational functions with holes

Converting repeating decimals in to fractions

Decimal representation of rational numbers

Finding square root using long division

L.C.M method to solve time and work problems

Translating the word problems in to algebraic expressions

Remainder when 2 power 256 is divided by 17

Remainder when 17 power 23 is divided by 16

Sum of all three digit numbers divisible by 6

Sum of all three digit numbers divisible by 7

Sum of all three digit numbers divisible by 8

Sum of all three digit numbers formed using 1, 3, 4

Sum of all three four digit numbers formed with non zero digits

Sum of all three four digit numbers formed using 0, 1, 2, 3

Sum of all three four digit numbers formed using 1, 2, 5, 6