COMBINING TRANSFORMATIONS WITH DILATIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
When creating an animation, figures need to be translated, reflected, rotated, and sometimes dilated. In this section, we are going to see, how different types of transformations can be combined with dilations.
Example :
A rectangle has the vertices (-6, 8), (-2, 8), (-2, 6) and (-6, 6). Apply the indicated series of transformations to the triangle. Each transformation is applied to the image of the previous transformation, not the original figure. Label each image with the steps of the transformation applied.
(i) (x, y) → (x + 7, y - 2)
(ii) Reflection across the x-axis.
(iii) Clockwise rotation of 90° around the origin
(iv) (x, y) → (x + 5, y + 3)
(v) Dilation about the origin with scale factor 3.
Compare the size and shape of the final image to that of the original figure.
Solution :
Step 1 :
(i) (x, y) → (x + 7, y - 2).
(-6, 8) -----> (1, 6)
(-2, 8) -----> (5, 6)
(-2, 6) -----> (5, 4)
(-6, 6) -----> (1, 4)
Graph the image.
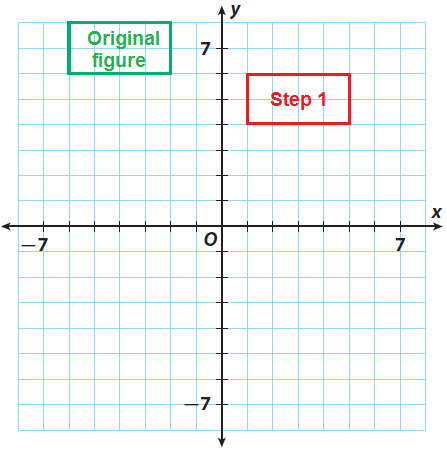
Step 2 :
(ii) Reflection across the x-axis.
Since there is a reflection across the x-axis, we have to multiply each y-coordinate by -1. That is,
(x, y) -----> (x, -y)
So, we have
(1, 6) -----> (1, -6)
(5, 6) -----> (5, -6)
(5, 4) -----> (5, -4)
(1, 4) -----> (1, -4)
Graph the image.
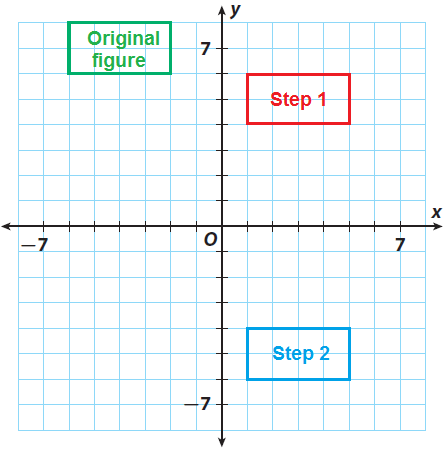
Step 3 :
(iii) Clockwise rotation of 90° around the origin.
Since there is a rotation of 90° clockwise about the origin, we have multiply each x-coordinate by -1 and interchange x and y coordinates. That is,
(x, y) -----> (y, -x)
So, we have
(1, -6) -----> (-6, -1)
(5, -6) -----> (-6, -5)
(5, -4) -----> (-4, -5)
(1, -4) -----> (-4, -1)
Graph the image.
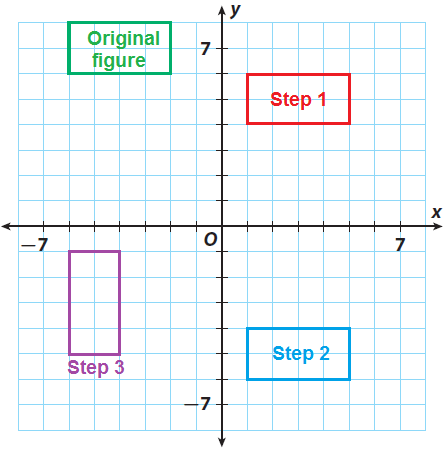
Step 4 :
(iii) (x, y) → (x + 5, y + 3)
(-6, -1) -----> (-1, 2)
(-6, -5) -----> (-1, -2)
(-4, -5) -----> (1, -2)
(-4, -1) -----> (1, 2)
Graph the image.
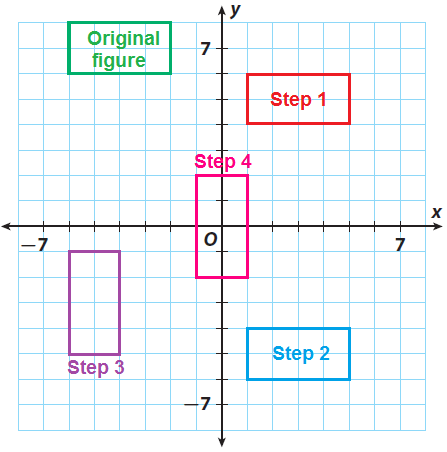
Step 5 :
(iii) (x, y) → (3x, 3y)
(-1, 2) -----> (-3, 6)
(-1, -2) -----> (-3, -6)
(1, -2) -----> (3, -6)
(1, 2) -----> (3, 6)
Graph the image.
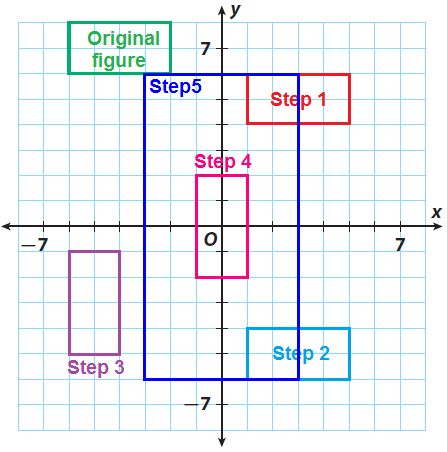
Compare the size and shape of the final image to that of the original figure.
Shape :
Same shape
Size :
The sides of rectangle E are three times the lengths of the sides of the original figure.
Angle Measures :
Same angle measures
Reflect
1. Which transformation represents the dilation? How can you tell?
(x, y) → (3x, 3y) ;
The algebraic form of a dilation is
(x, y) → (kx, ky)
In this case, k = 3.
2. A sequence of transformations containing a single dilation is applied to a figure. Are the original figure and its final image congruent? Explain.
No
The dilation would shrink or expand the figure so that it and its final image would not be the same size.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
