EXAMPLE PROBLEMS ON SURFACE AREA WITH COMBINED SOLIDS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :
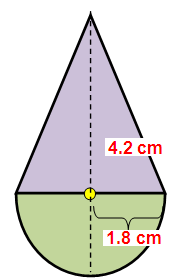
A play top is in the form of a hemisphere surmounted on a cone.
The diameter of the hemisphere is 3.6 cm. The total height of the play
top is 4.2 cm. Find its total surface area.
Solution :
Let r and h are radius and height of the cone.
diameter of the hemisphere = 3.6 cm
radius of hemisphere (r) = 3.6/2 = 1.8 cm
total height of the play top = 4.2cm
radius of hemisphere + height of cone = 4.2
1.8 + h = 4.2
h = 4.2-1.8
h = 2.4 cm
Now we are going to find slant height of cone
l2 = r2+h2
= (1.8)2+ (2.4)2
= 3.24 + 5.76
l2 = 9
L = √(3 ⋅ 3)
L = 3 cm
To find the total surface area of the play top, we have to find the sum of curved surface area of hemisphere and curved surface area of cone.
Total surface area of play top = C.S.A of hemisphere + C.S.A of cone
= 2Πr2+Πrl
= Πr(2r+l)
= Π ⋅ (1.8) [2(1.8) + 3]
= Π ⋅ (1.8) (3.6+3)
= Π (1.8) (6.6)
= 11.88 Π cm2
Total surface area of the play top = 11.88 Π cm².
Example 2 :
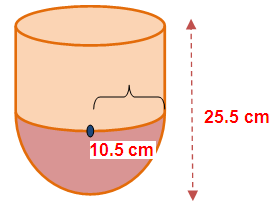
A solid is in the shape of a cylinder surmounted on a hemisphere. If the diameter and the total height of the solid are 21 cm,25.5 cm respectively, then find its volume.
Solution :
Let r and h are radius and height of the cylinder.
diameter of the hemisphere = 21 cm
radius of hemisphere (r) = (21)/2 = 10.5 cm
Total height of the solid shape = 25.5 cm
radius of hemisphere + height of the cylinder = 25.5
10.5 + h = 25.5
h = 25.5-10.5
h = 15 cm
To find the volume of the solid shape we have to find the sum of volume of hemisphere and volume of cylinder.
Volume of solid toy = Volume of hemisphere + Volume of cylinder
= (2/3) Πr3 + Π r2h
= Πr2[(2/3) r + h]
= (22/7) x (10.5)² [(2/3) 10.5 + 15]
= (22/7) ⋅ 10.5 ⋅ 10.5 (2(3.5)+15)
= 22 ⋅ 1.5 ⋅ 10.5 ⋅ (7+15)
= 7623 cm3
Volume of solid shape = 7623 cm3.
Example 3 :
A capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends. If the length of the entire capsule is 14 mm and diameter of the capsule is 5 mm, find its surface area.
Solution :
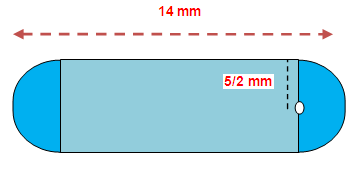
diameter of the hemisphere = 5 mm
radius of hemisphere (r) = 5/2 = 2.5 mm
total height of the solid = 14 mm
2(radius of hemisphere)+height of cylinder = 14
2 (5/2)+h = 14
5+h = 14
h = 14-5
h = 9 mm
Now we have to find total surface area of capsule. For that we have to find the sum of surface areas of two hemispheres and one cylinder.
Total surface area of capsule
= 2(CSA of hemisphere) + CSA of cylinder
= 2(2 Π r2)+2Πrh
= 2Πr(2r+h)
= 2⋅ (22/7)⋅ (2.5) [2(2.5)+9]
= (22/7) ⋅ 5⋅ (5+9)
= (110/7) (14)
= 220 mm2
Total surface area of capsule = 220 mm2.
Example 4 :
A tent is in the shape of right circular cylinder surmounted by a cone. The total height and diameter of the base are 13.5 m and 28 m. If the height of the cylindrical portion is 3 m, find the total surface area of the tent.
Solution :
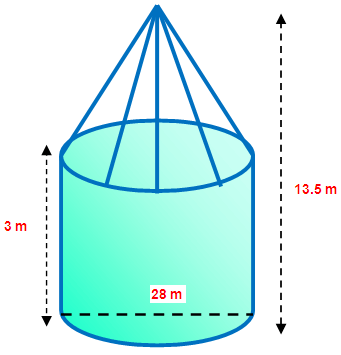
The total height of the tent = 13.5 m
The diameter of the base of the tent = 28 m
radius of the tent = 14 m
Height of cylindrical portion = 3 m
Total height of the tent = 13.5 m
Height of cylinder + Height of cone = 13.5
3+h = 13.5
h = 13.5-3
h = 10.5 m
height of cylindrical portion is 10.5 m
l2 = r2+h2
= 142+10.52
= 196+110.25
l = √306.25
l = 17.5
Total surface area of tent = CSA of cylinder + CSA area of cone
= 2Πrh + Πrl
= Πr(2h+l)
= (22/7) ⋅ 14 [2(3)+17.5]
= 22 ⋅ 2(6+17.5)
= 44 (23.5)
= 1034 cm3
Example 5 :
Using clay, a student made a right circular cone of height 48 cm and base radius 12 cm. Another student reshapes it in the form of a sphere. Find the radius of the sphere.
Solution :
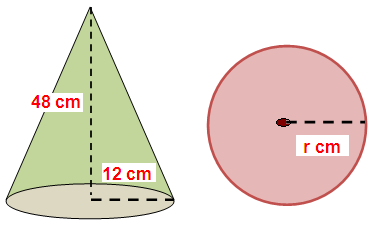
Height of the right circular cone (h) = 48 cm
Radius of right circular cone (r) = 12 cm
Volume of right circular cone = Volume of sphere
(1/3) Πr2h = (4/3) Πr3
(1/3) r2h = (4/3) r3
(1/3) (12)2(48) = (4/3) r3
(1/3) ⋅ 12 ⋅ 12 ⋅ 48 = (4/3) r3
r3 = (1/3) ⋅ 12 ⋅ 12 ⋅ 48 ⋅ (3/4)
r3 = 3 ⋅ 12 ⋅ 48
r = ∛ (3⋅3⋅4⋅4⋅4⋅3)
r = 12 cm
Radius of sphere is 12 cm.
Example 6 :
One quart of water-resistant paint covers 75 square feet. A swimming pool is in the shape of a rectangular prism with a length of 20 feet, a width of 10 feet, and a height of 5 feet. How many quarts should you buy to paint the swimming pool with two coats of paint?
Solution :
Area of the rectangular prims to be painted
= 2(lw + wh + hl)
length = 20 feet, width = 10 feet and height = 5 feet
= 2(20 x 10 + 10 x 5 + 5 x 20)
= 2(200 + 50 + 100)
= 2(350)
= 700 square feet
1 quart of paint will cover = 75 square feet
Number of quarts of paint = 700 / 75
= 9.33
approximately 10 quart of paint is needed.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
Quantitative Reasoning Questions and Answers
Dec 13, 25 12:45 PM
Quantitative Reasoning Questions and Answers -
Coin Tossing Probability
Dec 13, 25 10:11 AM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems -
10 Hard SAT Math Questions (Part - 39)
Dec 11, 25 05:59 PM
10 Hard SAT Math Questions (Part - 39)