COMBINATION OF SOLID SHAPES PROBLEMS

Problem 1 :

The radius of a solid sphere us 24 cm. It is melted and drawn into a long wire of uniform cross section. Find the length of the wire if its radius is 1.2 mm.

Solution :

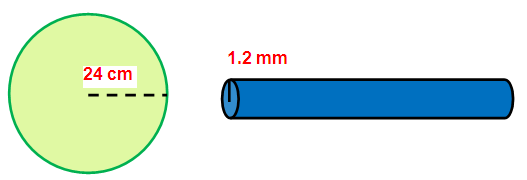
Radius of the solid sphere  =  24 cm

Radius of the wire  =  1.2 mm

Now we have to convert the radius of wire from mm to cm.

r  =  1.2/10 ==> 0.12 cm

Now we need to find the length of the wire that is height of the wire. after melted the sphere and drawn into a long wire of uniform cross section

Volume of sphere  =  Volume of cylindrical shaped wire

(4/3) Πr³  =  Π r² h

(4/3) r³  =  r² h

(4/3) (24)³  =  (0.12)² h

h  =  (4/3) (24)³/(0.12)²

h  =  (4/3) ⋅ 24 ⋅ 24 ⋅ 24 ⋅ (1/0.12) ⋅ (1/0.12)

h  =  4 ⋅ 8 ⋅ 200 ⋅ 200

h  =  1280000 mm

Now we have to convert this from mm to km

h  =  1280000/100000

h  =  12.8 km

So, the required height height is 12.8 km.

Problem 2 :

A right circular conical vessel whose internal radius is 5 cm and height is 24 cm is full of water. The water is emptied into an empty cylindrical vessel with internal radius 10 cm. Find the height of the water level in the cylindrical vessel.

Solution :

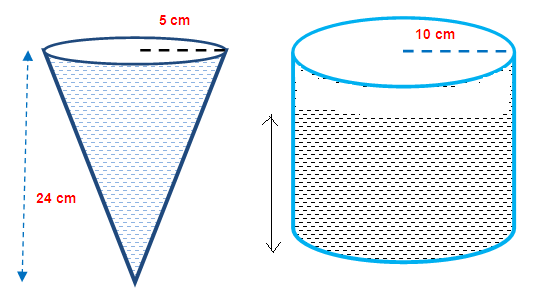
Radius of the right circular cone  =  5 cm

Height of right circular cone  =  24 cm

Radius of cylindrical tank  =  10 cm

Now we have to find the height of the cylindrical tank

 Volume of water inside the conical container  =  Volume of water in the cylindrical tank

(1/3) Π r² h  =  Π r² h

(1/3) 5² ⋅24  =  10² h

(1/3) ⋅ 5 ⋅ 5 ⋅ 24  =  10 ⋅ 10 ⋅h

h  =  (1/3) ⋅ 5 ⋅ 5 ⋅ 24/(10 ⋅ 10)

h  =  8/4

h  =  2 cm

So, height of water is 2 cm.

Problem 3 :

A solid sphere of diameter 6 cm is dropped into a right circular cylindrical vessel with diameter 12 cm, which is partly filled with water, If the sphere is completely submerged in water, how much does the water level in the cylindrical vessel.

Solution :

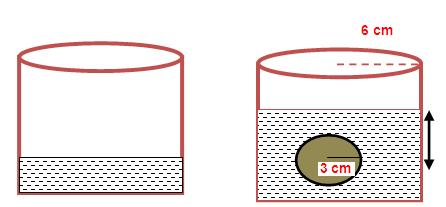
Diameter of sphere = 6 cm

Radius of sphere = 3 cm

diameter for cylindrical vessel = 12 cm

Radius of cylindrical vessel = 6 cm

Volume of water level increased in the cylindrical tank

=  Volume of sphere dropped into the vessel

Πr²h  =  (4/3)Πr³ 

r²h  =  (4/3) r³

6² ⋅ h  =  (4/3)(3)²

6 ⋅ 6 ⋅ h  =  (4/3) ⋅ 3 ⋅ 3 ⋅ 3

h  =  (4/3) ⋅ 3 ⋅ 3 ⋅  3 / (6 ⋅ 6)

h  =  1 cm

Therefore increased water level is 1 cm.

Problem 4 :

Though a cylindrical pipe of internal radius 7 cm, water flows out at the rate of 5 cm/sec. Calculate the volume of water (in liters) discharged through the pipe in half an hour.

Solution :

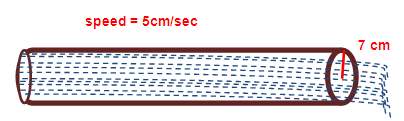
Now we need to find volume of water (in liters) discharged through the pipe in half an hour.

For that, let us convert speed into seconds.

half an hour  =  30 minutes

30 ⋅ 60  =  1800 seconds.

Volume of water discharged in half an hour 

=  Area of cross section ⋅  time ⋅ speed

=  Π r² ⋅ 5 ⋅ 1800

=  (22/7) ⋅  7² ⋅ 5 ⋅ 1800 

=  (22/7) ⋅ 7 ⋅ 7 ⋅ 5 ⋅ 1800

=  22 ⋅ 7 ⋅ 5 ⋅ 1800

=  1386000 cubic cm

But here we have to find volume of water discharged in liters.

For that we have to use the following conversion that is

1000 cm³  =  1 liter

=  1386000/1000

=  1386 liter

So, the quantity of water discharged is 1386 liters.

Problem 5 :

Water in a cylindrical tank of diameter 4 m and height 10 m is released through a cylindrical pipe of diameter 10 cm at the rate of 2.5 km/hr. How much time will it take to empty the half of  the tank? Assume that the tank is full of water to begin with.

Solution :

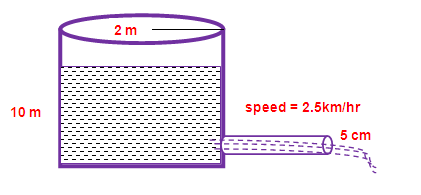
Now we are going to convert every measurements into m

Diameter of the cylindrical tank  =  4 m

radius of the cylindrical tank  =  2 m

height of the tank  =  10 m

Diameter of the cylindrical pipe  =  10 cm

radius of the cylindrical pipe  =  10/2  =  5 cm

=  5/100 m

speed of water  =  2.5 km/hr

1000 m  =  1 km

=  2.5 x 1000

Now we are going to convert every measurements into m

Diameter of the cylindrical tank = 4 m

radius of the cylindrical tank = 2 m

height of the tank = 10 m

Diameter of the cylindrical pipe = 10 cm

radius of the cylindrical pipe = 10/2 = 5 cm

                                                   = 5/100 m

speed of water = 2.5 km/hr

1000 m = 1 km

=  2.5 x 1000

=  2500 m/hr

Volume of water discharged from the cylindrical pipe 

=  (1/2) Volume of cylindrical tank

Area of cross section ⋅ time ⋅ speed  =  (1/2) Πr² h

                         Π r²⋅ time ⋅ speed  =  (1/2) Π r² h

             (5/100)²⋅ time ⋅ 2500  =  (1/2) ⋅ 2²⋅ 10

(5/100) ⋅ (5/100) ⋅ time ⋅ 2500  =  (1/2)⋅ 2⋅2⋅10

Time  =  2 ⋅ 10 ⋅ (100/5) ⋅ (100/5) ⋅ 1(1/2500)

Time  =  80/25

=  3.2 hour

1 hour = 60 minute

=  192 minute

=  180+12

3 hour and 12 minute     

So, time taken to empty the half of  the tank is 3 hour and 12 minute.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.