COEFFICIENT OF VARIATION FOR UNGROUPED DATA
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Formula for Coefficient of Variation :
C.V = (σ/x̄) ⋅ 100%
Example 1 :
Find the coefficient of variation of 24, 26, 33, 37, 29, 31.
Solution :
First let us find the standard deviation for the given data. For that, let us arrange the given data in ascending order.
24, 26, 29, 31, 33, 37
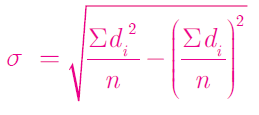
|
x 24 26 29 31 33 37 |
d = x - A d=x-31 -7 -5 -2 0 2 6 |
d2 48 25 4 0 4 36 |
Σd2/n = 117/6
(Σd/n)2 = (-6/6)2 = 1
σ = √(19.5 - 1)
= √18.5
σ = 4.30
x̄ = Σx/n
= (24 + 26 + 29 + 31 + 33 + 37)/6
x̄ = 180/6
x̄ = 30
Coefficient of variation (C.V) = (σ/x̄) ⋅ 100%
C.V = (4.30/30) ⋅ 100%
C.V = 0.143 ⋅ 100%
C.V = 14.33%
Hence the coefficient of variation of the given data is 14.4%
Example 2 :
The time taken (in minutes) to complete a homework by 8 students in a day are given by 38, 40, 47, 44, 46, 43, 49, 53. Find the coefficient of variation.
Solution :
38, 40, 43, 44, 46, 47, 49, 53
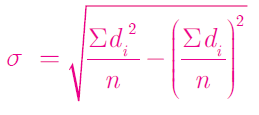
|
x 38 40 43 44 46 47 49 53 |
d = x - A d=x-44 -6 -4 -1 0 2 3 5 9 |
d2 36 16 1 0 4 9 25 81 |
Σd2/n = 172/8
(Σd/n)2 = (8/8)2 = 1
σ = √(21.5 - 1)
= √20.5
σ = 4.53
x̄ = Σx/n
= (38+40+43+44+46+47+49+53)/8
x̄ = 360/8
x̄ = 45
Coefficient of variation (C.V) = (σ/x̄) ⋅ 100%
C.V = (4.52/45) ⋅ 100%
C.V = 0.1006 ⋅ 100%
C.V = 10.07%
Hence the coefficient of variation of the given data is 10.07%
Example 3 :
The total marks scored by two students Sathya and Vidhya in 5 subjects are 460 and 480 with standard deviation 4.6 and 2.4 respectively. Who is more consistent in performance?
Solution :
Sathya
Sum of marks in 5 subjects = 460
mean mark of Sathya (x̄) = Σx/n = 460/5 = 92
Standard deviation (σ) = 4.6
Coefficient of variation (C.V) = (σ/x̄) ⋅ 100%
C.V = (4.6/92) ⋅ 100%
C.V = 0.05 ⋅ 100%
C.V = 5%
Vidhya :
Sum of marks in 5 subjects = 480
mean mark of Sathya (x̄) = Σx/n = 480/5 = 96
Standard deviation (σ) = 2.4
Coefficient of variation (C.V) = (σ/x̄) ⋅ 100%
C.V = (2.4/96) ⋅ 100%
C.V = 0.25 ⋅ 100%
C.V = 25%
Hence we decide that Vidhya is more consistent.
Example 4 :
Following are marks obtained, out of 100 by two students Andrew and Frad in 10 tests.
Scores of Andrew :
25, 50, 45, 30, 70, 42, 36, 48, 35, 60
Scores of Frad :
10, 70, 50, 20, 95, 55, 42, 60, 48, 80
Who is more intelligent and who is more consistent ?
Solution :
Calculating standard deviation for Andrew :
|
x 25 50 45 30 70 42 36 48 35 60 |
d = x - A d=x-42 -17 8 3 -12 28 0 -6 6 -7 18 |
d2 289 64 9 144 784 0 36 36 49 324 |
Σd2 = 289 + 64 + 9 + 144 + 784 + 0 + 36 + 36 + 49 + 324
= 1735
Σd = (-17) + 8 + 3 + (-12) + 28 + 0 + (-6) + 6 + (-7) + 18
= -42 + 63
= 21
Calculating mean for Andrew :
x̄ = (25 + 50 + 45 + 30 + 70 + 42 + 36 + 48 + 35 + 60) / 10
= 441/10
= 44.1
Calculating standard deviation for Frad :
|
x 10 70 50 20 95 55 42 60 48 80 |
d = x - A d=x-55 -45 15 -5 -35 40 0 -13 5 -7 25 |
d2 2025 225 25 1225 1600 0 169 25 49 625 |
Σd2 =2025 + 225 + 25 + 1225 + 1600 + 0 + 169 + 25 + 49 + 625
= 5968
Σd = -45 + 15 + (-5) + (-35) + 40 + 0 + (-13) + 5 + (-7) + 25
= -105 + 85
= -20
Calculating mean for Frad :
x̄ = (10+70+50+20+95+55+42+60+48+80) / 10
= 530/10
= 53
Coefficient of variation of Andrew :
= (Standard deviation / mean) x 100%
= (σ/x̄) x 100%
= (13.003/44.1) x 100%
= (0.294) x 100%
= 29.4%
Coefficient of variation of Frad :
= (Standard deviation / mean) x 100%
= (σ/x̄) x 100%
= (24.34/53) x 100%
= (0.459) x 100%
= 45.9%
Frad has greater coefficient of variation, then he is intelligent and consistent.
Example 5 :
Coefficient of variation of two distributions are 50 and 60, and their arithmetic means are 30 and 25 respectively. Difference of their standard deviation is
(A) 0 (B) 1 (C) 1.5 (D) 2.5
Solution :
Coefficient of variation = (σ/x̄) x 100%
Finding standard distribution for first data :
Applying coefficient of variation as 50 and mean as 30, we get
50 = (σ/30) x 100%
50 = (σ/30)
σ = 50(30)
σ = 1500
Finding standard distribution for second data :
Applying coefficient of variation as 60 and mean as 25, we get
60 = (σ/25) x 100%
60 = (σ/25)
σ = 60(25)
σ = 1500
Difference between two standard deviations
= 1500 - 1500
= 0
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 06, 26 04:54 AM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

