CLOCK PROBLEMS

Minutes are Gained 

It is nothing but the minute spaces between the two hands.

When we calculate minute spaces between the two hands , we have to consider the following points.

1. We have to measure minute spaces from hour hand to minute hand in clock wise direction.

2. If the two hands are coincident, and we want the minute spaces between them to be 10 minutes, then 10 minutes to be gained.

3. If there is 10 minutes spaces between the two hands and we want them to be coincident, then 10 minutes to be gained.

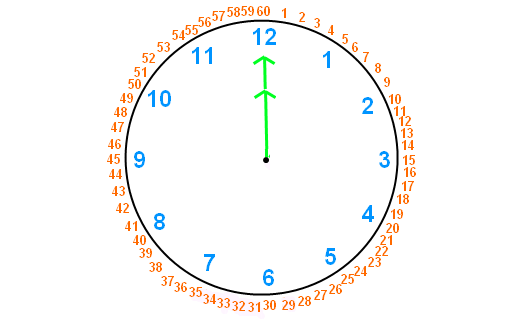
In the above clock,  the two hands are coincident and the time is 12'o clock. The minute spaces between the two hands is zero. If the minute hand traces 60 minutes, the time will be 1'o clock. That has been shown in the clock below.

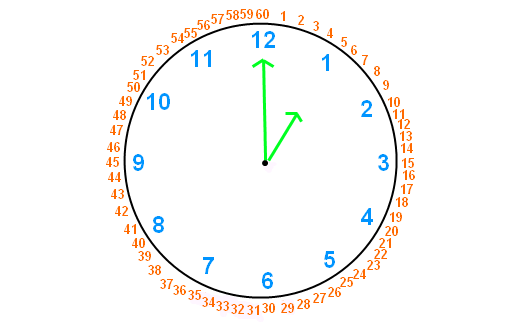
From the first clock to second clock, when the minute hand traces 60 minutes, the minute spaces between the hour hand and minute hand becomes 55 in the second clock from zero in the first clock.

From this, it is very clear, to gain 55 minutes (head of hour hand), minute hand must trace 60 minutes.

So, 55 minutes are gained in 60 minutes.

1 minute is gained in

= ⁶⁰⁄₅₅

= ¹²⁄₁₁ minutes

No. of minutes taken > No. of minutes gained

Solved Problems

Problem 1 : 

Find the angle between the hour hand and minute hand of a clock when the time is 4.20?

Solution :

Angle traced by the hour hand in 12 hours is 360°.

Angle traced by the hour hand in 1 hour is 

= ³⁶⁰^°⁄₁₂

= 30°

4 hrs 20 min = 4²⁰⁄₆₀ = 4⅓ = ¹³⁄₃ hrs

Angle traced by 4 hrs 20 min is 

=  30° x ¹³⁄₃

= 130°

Angle traced by the minute hand in 60 minutes is 360°.

Angle traced by the minute hand in 1 minute is 

= ³⁶⁰^°⁄₆₀

= 6°

Angle traced by the minute hand in 20 min is

= 20 x 6°

= 120°

Angle between the two hands is 

= Difference between the angles traced by the two hands.

So, the angle between the two hands is 

= 130° - 120°

= 10°

At 4.20, the angle between the hour hand and minute hand is 10°.

Problem 2 : 

At what time (in minutes), between 3 o'clock and 4 o'clock, both the needles will coincide each other ?

Solution :

At 3 o'clock, the minute spaces between minute hand and hour hand is 15 minutes.

To be coincident, the minute hand must must gain 15 min.spaces.

1 minute is gained in 12/11 minutes (see the notes).

15 minutes are gained in

=  15 x ¹²⁄₁₁ min

= ¹⁸⁰⁄₁₁ min

= 16⁴⁄₁₁ min.

So, the hands are coincident at 3 hrs 16⁴⁄₁₁ minutes.

Problem 3 :

How many times do the hands of a clock coincide in a day?

Solution :

The hands of a clock coincide in the following timings.

12'o clock ----> 1

1 to 2 ----> 2

2 to 3 ----> 3

3 to 4 ----> 4

4 to 5 ----> 5

5 to 6 ----> 6

6 to 7 ----> 7

7 to 8 ----> 8

8 to 9 ----> 9

9 to 10 ----> 10

10 to 11 ----> 11

From the above calculation, it is very clear that the hands coincide 11 times in 12 hours.

In 24 hours, they coincide 22 times.

So, the hands of a clock coincide 22 times in a day.

Problem 4 : 

How many times in a day, are the hands of a clock in straight line but opposite in direction ?

Solution :

The hands of a clock point in opposite direction in the following timings.

6'o clock ----> 1

7 to 8 ----> 2

8 to 9 ----> 3

9 to 10 ----> 4

10 to 11 ----> 5

11 to 12 ----> 6

12 to 1 ----> 7

1 to 2 ----> 8

2 to 3 ----> 9

3 to 4 ----> 10

4 to 5 ----> 11

From the above calculation, it is very clear that the hands point in opposite directions 11 times in 12 hours.

In 24 hours, they point in opposite directions in 22 times.

So, they point in opposite directions 22 times in a day.

Problem 5 : 

At what time between 4 and 5 o'clock will the hands of a watch point in opposite directions ?

Solution :

At 4 o'clock, min. spaces between hour hand and minute hand is 20.

To be in opposite directions, there must be 30 min. spaces between the two hands.

If 20 minutes are gained, the hands would be coincident.

But we need 30 min. spaces between the hands for being opposite in directions.

So, 30 more minutes to be gained when the are coincident.

In total, 50 minutes (20 + 30 = 50) to be gained for the hands to be opposite in directions.

1 minute is gained in 12/11 minutes.

50 minutes are gained in

=  50 x ¹²⁄₁₁ minutes

=  54⁶⁄₁₁ minutes

So, between 4 and 5 o'clock the hands of a clock point in opposite directions at 4 hrs 54⁶⁄₁₁ minutes.

Problem 6 : 

How many times are the hands of a clock at right angle in a day?

Solution :

Number of times of right angle between the two hands in the following timings.

12 to 1 ----> 2 times

1 to 2 ----> 2 times

2 to 3 ----> 2 times (right angle at 3'o clock included)

3 to 4 ----> 1 time (right angle at 3'o clock not included)

4 to 5 ----> 2 times

5 to 6 ----> 2 times

6 to 7 ----> 2 times

7 to 8 ----> 2 times

8 to 9 ----> 2 times (right angle at 9'o clock included)

9 to 10 ----> 1 time (right angle at 9'o clock not included)

10 to 11 ----> 2 times

11 to 12 ----> 2 times

From the above calculation, it is clear that the hands are at right angle 22 times in 12 hours.

In 24 hours, the hands are at right angle in 44 times.

So, the hands of a clock at right angle 44 times in a day. 

Problem 7 : 

Find the reflex angle between the hands of a clock at 10.25. 

Solution :

(Hint : To find the reflex angle between the hands, find the actual angle between the hands and subtract it from 360°)

10 hrs 25 min = 10²⁵⁄₆₀ = 10⁵⁄₁₂ = ¹²⁵⁄₁₂ hrs

Angle traced by the hour hand in 1 hour is 

= ³⁶⁰^°⁄₁₂

= 30°

Angle traced by 10 hrs 25 min is 

= (¹²⁵⁄₁₂) x 30

= 312½°

Angle traced by the minute hand in 1 minutes is

= ³⁶⁰^°⁄₆₀

= 6°

Angle traced by the minute hand in 25 min is 

= 25 x 6°

= 150°

Angle between the two hands is

= Difference between the angles traced by the two hands.

= 312½° - 150°

= 162½°

Reflex angle is 

= 360° - 162½°

= 197½°

So, the reflex angle between the hands of a clock at 10.25 is 197½°. 

Problem 8 : 

At what time between 4 and 5'o clock will the hands of a clock be at right angle (approximately)?

Solution :

At 4'o clock, the minute hand will be 20 min. spaces behind the hour hand.

If we want them to be at right angle, they have to be 15 min. spaces apart.

So they would be at right angle in the following two cases.

Case 1 :

When the minute hand is 15 min. spaces behind the hour hand,minute hand must gain (20 - 15) = 5 minutes.

1 minute is gained in ¹²⁄₁₁ minutes.

5 minutes are gained in

= 5 x ¹²⁄₁₁ min

= 5⁵⁄₁₁ minutes

They are at right angles at 4 hrs 5⁵⁄₁₁ minutes.

Case 2 :

When the minute hand is 15 min. spaces ahead of the hour hand, minute hand must gain 5 minutes (20 + 15 = 35).

1 minute is gained in ¹²⁄₁₁ minutes.

35 minutes are gained in

= 35 x ¹²⁄₁₁ min

= 38²⁄₁₁ minutes

They are at right angles at 4 hrs 38²⁄₁₁ minutes.

So, the hands would be at right angles at 4 hrs 5⁵⁄₁₁ minutes and 4 hrs 38²⁄₁₁ minutes.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.