CLASSIFYING TRIANGLES BY SIDES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Triangles can be classified into three types by their sides.
1. Equilateral triangle
2. Isosceles triangle
3. Scalene triangle
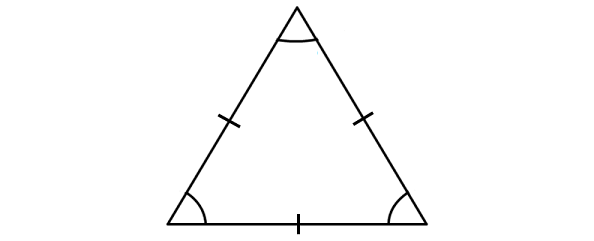
Equilateral Triangle
An equilateral triangle is a triangle with three congruent sides.
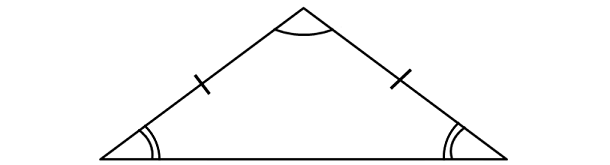
Isosceles Triangle
An equilateral triangle is a triangle with at least two congruent sides.
Scalene Triangle
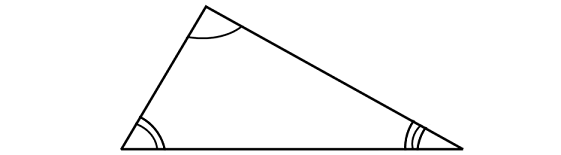
An equilateral triangle is a triangle with no congruent sides.
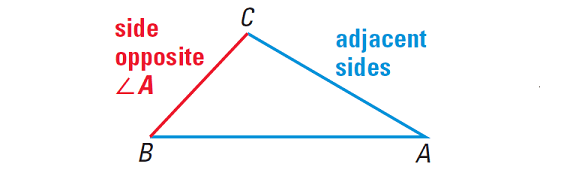
Each of the three points joining the sides of a triangle is a vertex. (The plural form of vertex is vertices) For example, in the triangle ABC shown below, points A, B and C are vertices.
In a triangle, two sides sharing a common vertex are adjacent sides. In triangle ABC shown below, CA and BA are adjacent sides. The third side BC is the side opposite to ∠A.
Right and Isosceles Triangles
The sides of right triangles and isosceles triangles have special names. In a right triangle, the sides that form the right angle are the legs of the right triangle. The side opposite to the right angle is the hypotenuse of the triangle.
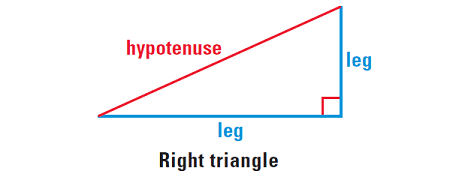
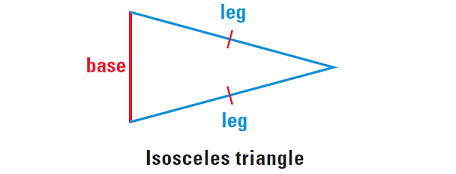
An isosceles triangle can have three congruent sides, in that case it is equilateral. When an isosceles triangle has only two congruent sides, then these two sides are the legs of the isosceles triangle. The third side is the base of the isosceles triangle.
Solved Problems
Problem 1 :
Identify the type of triangle whose diagram is given below.
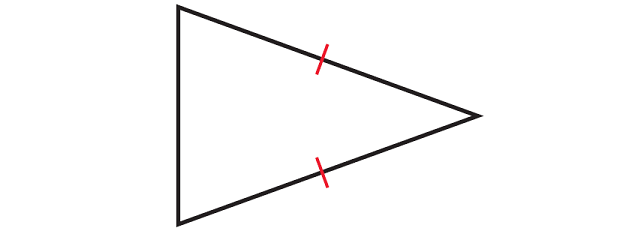
Solution :
In the triangle given above, two of the sides are congruent.
So, it is isosceles triangle.
Example 2 :
Identify the type of triangle whose diagram is given below.
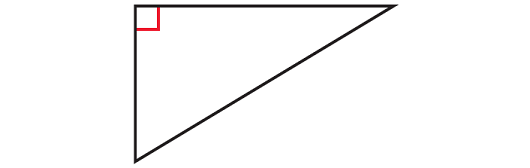
Solution :
In the triangle given above, one of the angles right angle. So, it is right triangle.
Note :
If one of the angles is right angle and two of the sides are congruent, it is right isosceles triangle.
Example 3 :
Identify the type of triangle whose diagram is given below.
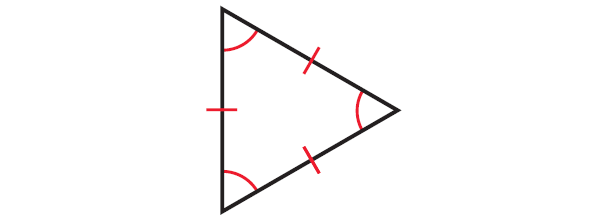
Solution :
In the triangle above, the lengths of all the three sides are same and all the three angles are congruent.
So, the given triangle is equilateral triangle.
Example 4 :
Is it possible to have a triangle whose sides are 5 cm, 6 cm and 4 cm ? If so, identify the type of triangle.
Solution :
Verify the property
'The sum of the lengths of any two sides of a triangle is always greater than the third side',
for the given three sides.
5 cm + 6 cm > 4 cm
6 cm + 4 cm > 5 cm
5 cm + 4 cm > 6 cm
Because the given sides meet the condition said in the property, it is possible to have a triangle whose sides are 5 cm, 6 cm and 4 cm.
All the three sides are different in length. So it is scalene triangle.
Example 5 :
Is it possible to have a triangle whose sides are 7 cm, 2 cm and 4 cm ? If so, identify the type of triangle.
Solution :
Verify the property
'The sum of the lengths of any two sides of a triangle is always greater than the third side',
for the given three sides.
2 cm + 4 cm < 7 cm
Because the given sides do not meet the condition said in the property, it is not possible to have a triangle whose sides are 7 cm, 2 cm and 4 cm.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

