CLASSIFYING TRIANGLES BY SIDES WORKSHEET

1. Identify the type of triangle whose diagram is given below.

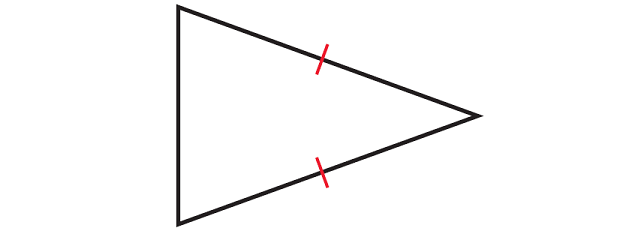
2. Identify the type of triangle whose diagram is given below.

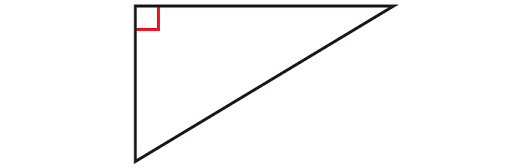
3. Identify the type of triangle whose diagram is given below.

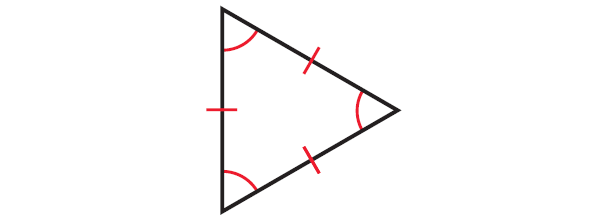
4. Is it possible to have a triangle whose sides are 5 cm, 6 cm and 4 cm ? If so, identify the type of triangle.

5. Is it possible to have a triangle whose sides are 7 cm, 2 cm and 4 cm ? If so, identify the type of triangle.

1. Answer :

In the triangle given above, two of the sides are congruent. So, it is isosceles triangle.

2. Answer :

In the triangle given above, one of the angles right angle. So, it is right triangle.

Note :

If one of the angles is right angle and two of the sides are congruent, it is right isosceles triangle.

3. Answer :

In the triangle above, the lengths of all the three sides are same and all the three angles are congruent.

So, the given triangle is equilateral triangle.

4. Answer :

Verify the property

"The sum of the lengths of any two sides of a triangle is always greater than the third side",

for the given three sides.

5 cm + 6 cm > 4 cm

6 cm + 4 cm > 5 cm

5 cm + 4 cm > 6 cm

Because the given sides meet the condition said in the property, it is possible to have a triangle whose sides are 5 cm, 6 cm and 4 cm.

All the three sides are different in length. So it is scalene triangle.

5. Answer :

Verify the property

"The sum of the lengths of any two sides of a triangle is always greater than the third side",

for the given three sides.

2 cm + 4 cm < 7 cm

Because the given sides do not meet the condition said in the property, it is not possible to have a triangle whose sides are 7 cm, 2 cm and 4 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.