CLASSIFYING THE DATA AS DISCREATE OR CONTINOUS

A quantitative variable is one which has a numerical value, and is often is called a numerical variable. The information collected is called numerical data.

Quantitative variable can be either discreate or continuous.

Example 1 :

State whether these quantitative (or numerical) variables are discrete or continuous :

a) the time taken to run 1500 metres

b) the maximum temperature reached on a March day

c) the weight of cargo taken on a ship

d) the time taken for a battery to run down

e) the number of trips made by a taxi

f) the number of people in a theatre

g) the number of minutes spent sending text messages per day

Solution :

(a)  Since time is measurable, it is continuous data.

(b)  Since temperature is measurable, it is continuous data.

(c)  Since weight is measurable, it is continuous data.

(d)  Since time is measurable, it is continuous data.

(e)  Since number of trips is countable, it is discrete data.

(f)  Since number of people is countable, it is discrete data.

(g)  Number of minutes is measurable, it is continuous data.

Example 2 :

20 students were asked “How many TV sets do you have in your household?” and the following data was collected:

2,  1,  0,  3,  1,  2,  1,  3, 4, 0, 0, 2, 2, 0, 1,  1,  0,  1,  0,  1

Is the data discrete or continuous? Why?

Solution :

The given data is discrete, because we cannot have part of TV.

Example 3 :

The function y = 15.95x represents the cost y (in dollars) of x tickets for the South Florida Museum. Graph the function using a domain of 0, 1, 2, 3, and 4.

Is the domain of the graph discrete or continuous?

Explain. Make an input-output table.

Solution :

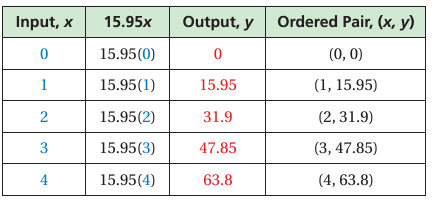
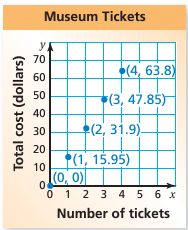
Plot the ordered pairs. Because you cannot buy part of a ticket, the graph consists of individual points.

So, the domain is discrete.

Example 4 :

A cereal bar contains 130 calories. The number c of calories consumed is a function of the number b of bars eaten. Graph the function.

Is the domain of the graph discrete or continuous?

Make an input-output table.

Solution :

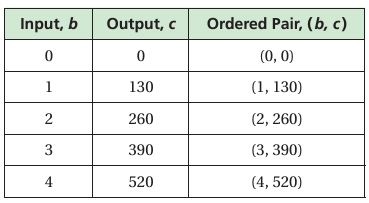
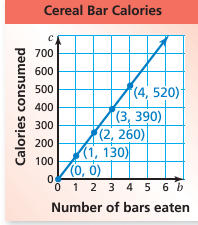
Plot the ordered pairs. Because you can eat part of a cereal bar, b can be any value greater than or equal to 0. Draw a line through the points.

So, the domain is continuous.

Example 5 :

You conduct an experiment on the speed of sound waves in dry air at 86 °F. You record your data in a table. Which of the following is true?

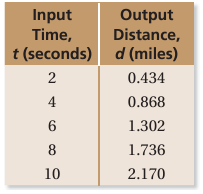
A)  The domain is t ≥ 2 and t ≤ 10 and it is discrete.

B) The domain is t ≥ 2 and t ≤ 10 and it is continuous.

C)  The domain is d ≥ 0.434 and d ≤ 2.17 and it is discrete.

D) The domain is d ≥ 0.434 and d ≤ 2.17 and it is continuous.

Solution :

The domain is the set of possible input values, or the time t. The time t can be any value from 2 to 10.

So, the domain is continuous. The correct answer is B.

Example 6 :

A 20-gallon bathtub is draining at a rate of 2.5 gallons per minute. The number g of gallons remaining is a function of the number m of minutes.

Is the domain discrete or continuous?

Solution :

Amount of water initially = 20 gallons

Amount of water draining out = 2.5 gallons per minute

Let m be the number of minutes. Then the required function will be

Quantity of water remaining = 20 - 2.5m

Domain is number of minutes, it is continuous.

Example 7 :

Are the data shown in the table discrete or continuous? Explain.

Solution :

The table shows the number of stories as whole numbers and it cannot be the decimal. Then, it must be discrete.

Example 8 :

The function m = 40 − 8.5b represents the amount m of money (in dollars) that you have after buying b balls of yarn. Graph the function using a domain of 0, 1, 2, and 3. Is the domain discrete or continuous?

Solution :

Domain is 0, 1, 2, 3.

When b = 0

m = 40 − 8.5(0)

m = 40

When b = 1

m = 40 − 8.5(1)

m = 31.5

When b = 2

m = 40 − 8.5(2)

m = 40 - 17

m = 23

When b = 3

m = 40 − 8.5(3)

m = 40 - 25.5

= 14.5

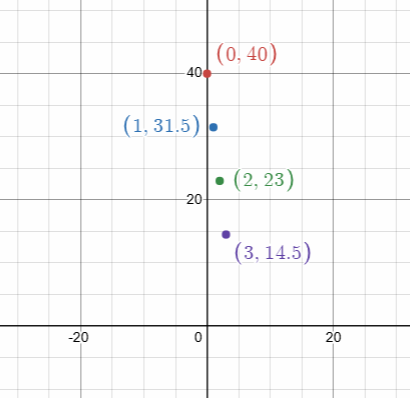
It is discrete, since it does not pass through origin.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.