CLASSIFYING RATIONAL NUMBERS

Students who are studying math in primary level must be aware of classification of rational numbers. 

We can use Venn diagram to classify rational numbers.

A Venn diagram is a visual representation used to show the relationships between groups.

The Venn diagram below shows how rational numbers, integers, and whole numbers are related. 

The following are the classifications of rational numbers. 

(i)  Natural Numbers :

N  =  { 1, 2, 3, 4, ...... }

(ii)  Whole Numbers :

W  =  { 0, 1, 2, 3, ....... }

(iii)  Integers :

Z  =  {.........-2, -1, 0, 1, 2, 3, .........} 

(iv)  Fractions :

Examples : -1/2, 7/3, 3/4, 2 1/7

(v)  Decimals :

Examples : 0.2, -1.23, 0.0085

(vi)  Recurring Decimal : 

Examples : 0.333333......, 0.257257..........

Caution : 

Non terminating recurring decimal is a rational number. 

Examples : 0.333333......, 0.257257..........

But, non terminating non recurring decimal is not a rational number and it is irrational number.

Examples: 

√2  =  1.41421356......................

√3  =  1.73205080....................

Solved Questions

Question 1 :

Place the following numbers in the Venn diagram. Then classify each number by indicating in which set or sets each number belongs.

0.35, -3, 75, 3/4

Solution :

75 : 

The number 75 belongs in the sets of whole numbers, integers, and rational numbers.

-3 :

The number -3 belongs in the sets of integers and rational numbers.

3/4 :

The number -3/4 belongs in the set of rational numbers.

0.35 :

The number 0.35 belongs in the set of rational numbers.

Question 2 :

Classify the following two numbers as rational and irrational and also explain your answer. 

5.312312312.......................

5.385164807.......................

Answer : 

5.312312312....................... ---> Rational number

5.385164807....................... ---> Irrational number

Explanation : 

Even though 5.312312312.......... is  a non terminating decimal, there is a repeated pattern 312 in it. 

So, 5.312312312....... is non terminating recurring decimal. 

Hence, 5.312312312....... is a rational number.  

5.385164807............ is  a non terminating decimal and also there is no repeated pattern in it. 

So, 5.385164807............ is non terminating non recurring decimal. 

Hence, 5.385164807............ is an irrational number.  

Question 3 : 

Why is the non terminating recurring decimal

2.0343434 .........

considered to be a rational number ? Explain.

Solution : 

Rational number is usually expressed in the form a/b. 

So, if we can express any number in the form "a/b", the number can be considered as rational number. 

Now, let us see, how to express the number 2.0343434...... in the form a/b, say fraction. 

Step 1 : 

Let  x  =  2.0343434...........

Step 2 : 

Identify the repeated pattern

In 2.0343434..........., the repeated pattern is 34

(Because 34 is being repeated)

Step 3 :

Identify the first repeated pattern and second repeated pattern as as explained below. 

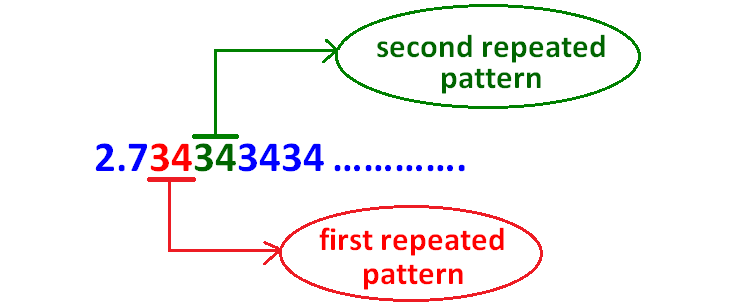
Step 4 :

Count the number of digits between the decimal point and first repeated pattern as given in the picture below. 

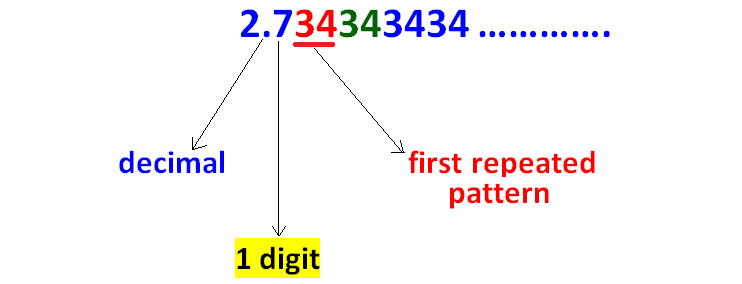
Step 5 :

Since there is 1 digit between the decimal point and the first repeated pattern, we have to multiply the given decimal by 10 as given in the picture below. 

(If there are two digits -----------> multiply by 100,

three digits -----------> multiply by 1000  and  so on )

Note :

In (1), we have only repeated patterns after the decimal.

Step 6 : 

Count the number of digits between the decimal point and second repeated pattern as given in the picture below.

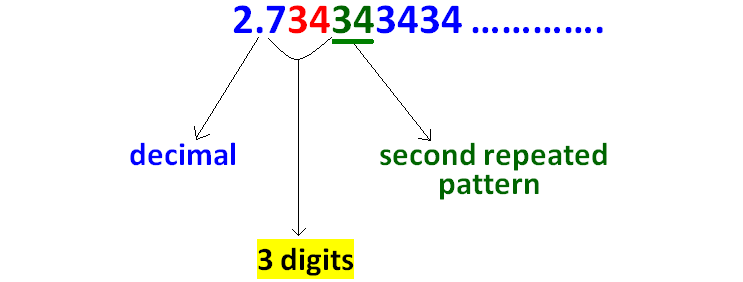
Step 7 :

Since there are 3 digits between the decimal point and the second repeated pattern, we have to multiply the given decimal by 1000 as given in the picture below. 

Note :

In (2), we have only repeated patterns after the decimal.

Step 8 :

Now, we have to subtract the result of step 5 from step 7 as given in the picture below. 

Now we got the fraction which is equal to the given decimal.

Because the given non terminating recurring decimal can be written as a fraction, it is considered to be a rational number.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.