CLASSIFYING POLYNOMIALS DEGREE AND COEFFICIENT OF TERMS WORKSHEET

Question 1 :

State which of the following expressions are polynomials in one variable or not. Give reasons for your answer.

(i)  2x5-x3+x-6

(ii)  3x2-2x+1

(iii)  y3+2√3

(iv)  x - 1/x

(v)  ∛t+2t

(vi)  x3 + y3 +z6

Question 2 :

Write the coefficient of x2 and x in each of the following:

(i)  2+3x-4x2+x3    (ii)  √3x + 1      (iii) x3 + √2x2+ 4x-1

(iv) 1/3 x² + x + 6

Question 3 :

Write the degree of each of the following polynomials.

(i) 4- 3x2        (ii)    5y+√2          (iii)  12-x+4x³    (iv)   5

Question 4 :

Classify the following polynomials based on their degree.

(i)  3x2 + 2x +1        (ii)  4x3 -1          (iii)  y+3

(iv)  y2-4             (v)   4x3           (vi)   2x

Question 5 :

Give one example of a binomial of degree 27 and monomial of degree 49 and trinomial of degree 36.

Question 6 :

Find the degree and number of terms of each polynomial.

a) 4w2

b) 9x3 + 2x

c) 4p5 - p3 + p5

Question 7 :

Fill in the blanks with monomial, binomial or trinomial

a)  A_____ is a polynomial with three terms

b) A _____ is a polynomial with one term.

c) A _____ is polynomial with two terms.

Question 8 :

Write each polynomial in standard form, then give the leading coefficient 

a) 12 + 3x2 - x

b) g4 - 2g3 - g5

c) k2 + k4 - k5 + 1

Question 9 :

classifying-polynomial-q1

a) I am a monomial with with degree 5, who i am ?

b)  I am the sum of monomials with degree 8, who i am ?

c)  I am a trinomial with degree 5, who i am ?

d)  I am a binomial, both my terms have degree, who i am ?

e)  I am monomial with degree 4, who i am ?

f)  I am binomial with degree 4, who i am ?

g) I am a trinomial, when you put me in standard form, my leading coefficient is -3, who i am?

(1)  Solution :

State which of the following expressions are polynomials in one variable or not. Give reasons for your answer.

(i)  2x5-x3+x-6

(ii)  3x2-2x+1

(iii)  y3+2√3

(iv)  x - 1/x

(i) Polynomial in one variable

(ii) Polynomial in one variable

(iii) Polynomial in one variable.

(iv)  Since the exponent of x is not a whole number, it is not a polynomial.

(v)  ∛t+2t

Since the exponent of t is not a whole number, it is not a polynomial.

(vi)  x3 + y3 +z6

Not a polynomial in one variable.

(2)  Solution :

Polynomial

2+3x-4x2+x3

√3x+1

x3+√2x2+4x-1

1/3 x²+x+6

Coefficient of x2

-4

0

√2

1/3

Coefficient of x

3

√3

4

x

(3)  Solution :

Polynomial

(i) 4- 3x2

(ii)    5y+√2

(iii)  12-x+4x³

(iv)   5

Degree

2

1

3

0

(4)  Solution :

(i)  3x2 + 2x +1

Since the degree of the polynomial is 2, it is a quadratic equation(polynomial).

(ii)  4x3-1

Since the degree of the polynomial is 3, it is a cubic equation(polynomial).

(iii)  y+3

Since the degree of the polynomial is 1, it is a linear polynomial.

(iv)  y2 - 4

Since the degree of the polynomial is 2, it is a quadratic polynomial.

(v)  4x3

Since the degree of the polynomial is 3, it is a cubic polynomial.

(vi) 2x

Since the degree of the polynomial is 1, it is a linear polynomial.

(5)  Solution :

Give one example of a binomial of degree 27 and monomial of degree 49 and trinomial of degree 36.

  • Binomial of degree 27  =  ax27+b
  • Monomial of degree  49  =  cy49
  • Trinomial of degree 36  =  ax36+ bx6 + cx

(6) Solution :

a) 4w2

The highest exponent of the polynomial is 2,

Degree = 2

Number of terms = 1

b) 9x3 + 2x

The highest exponent of the polynomial is 3,

Degree = 3

Number of terms = 2

c) 4p5 - p3 + p2 + 11

The highest exponent of the polynomial is 2,

Degree = 5

Number of terms = 4

(7) Solution :

(a)  The polynomial which has three terms is called trinomial. So,

A trinomial is a polynomial with three terms

b) The polynomial which has one term is called monomial. So,

A monomial is a polynomial with one term.

c) A polynomial which has two terms is called binomial. So,

A binomial is polynomial with two terms.

(8) Writing the polynomial which has the highest exponent to the lowest exponent is known as writing down the polynomial in standard form.

a) 12 + 3x2 - x

Standard form :

3x2 - x + 12

  • The highest exponent is 2, so degree is 2.
  • Coefficient of highest exponent term is 3, so leading coefficient is 3.

b) g4 - 2g3 - g5

Standard form :

- g5 + g4 - 2g3

  • The highest exponent is 5, so degree is 5.
  • Coefficient of highest exponent term is -1, so leading coefficient is -1.

c) k2 + k4 - k5 + 1

Standard form :

- k5 - k4 + k2  + 1

  • The highest exponent is 5, so degree is 5.
  • Coefficient of highest exponent term is -1, so leading coefficient is -1.

(9)  Solution :

classifying-polynomial-q1

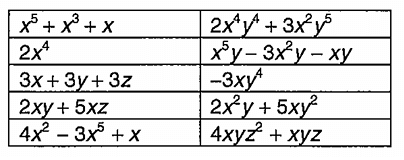
a) Monomial will have only one term, in -3xy4

Degree of -3xy4 = 1 + 4 ==> 5

b) Since the given is sum of monomials, we consider the sum of two monomials 

2x4 y4 + 3x2y5

degree = 4 + 4 ==> 8

Since the highest exponent can be considered as degree, the degree of the above polynomial is 8.

c)  Trinomial will consist of 3 terms,

x5 + x3 + 1

The degree of the polynomial is 5.

d)  2xy + 5xz 

e)  2x4

f)  4xyz2 + xyz

g) In the polynomial 4x2 - 3x5 + x

Writing in standard form, we get

- 3x5 +  4x2 + x

The leading coefficient is -3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

©All rights reserved. onlinemath4all.com

Recent Articles

RSS

  1. AP Calculus AB Problems with Solutions (Part - 23)

    May 21, 25 01:19 PM

    apcalculusab22.png
    AP Calculus AB Problems with Solutions (Part - 23)

    Read More

  2. Digital SAT Math Problems and Solutions (Part - 166)

    May 21, 25 05:33 AM

    digitalsatmath210.png
    Digital SAT Math Problems and Solutions (Part - 166)

    Read More

  3. Precalculus Problems and Solutions (Part - 13)

    May 20, 25 06:56 AM

    Precalculus Problems and Solutions (Part - 13)

    Read More