CLASSIFYING ANGLES WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
1. Classify the angles as acute, right, obtuse straight, reflex or full angle :
35°
135°
205°
180°
90°
360°
270°
2. If 4 times the sum of an angle and 5 is 32°, find the type of the angle.
3. If 2 times the sum of 3 times of an angle and 20 is 1024°, find the type of the angle.
4. If the sum of 5 times of an angle and 2 is 1222°, find the type of the angle.
5. If 5 times the difference between an angle and 22 is 440°, find the type of the angle.
6. If 7 times the difference between 3 times of an angle and 5 is 3745°, find the type of the angle.
7. If 2 times the difference between 9 times of angle and 15 is 6450°, find the type of the angle.
Classify and write the angles as acute, obtuse and right angle.
8.
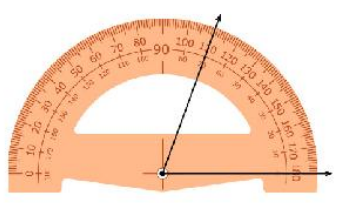
9.
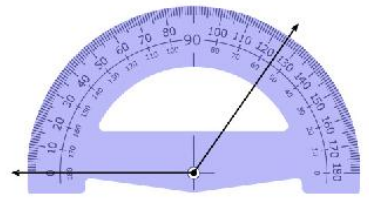
10.
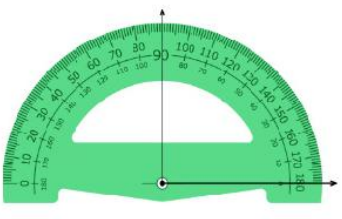
11. Classify the following angles (acute angle, obtuse angle and right angle)
30°, 45°, 60°, 90°, 120°, 130°, 170°, 75°
12. The angles below 90° and above 0° are called as ________
13. The angles belo 180° awnd above 90° are called as _________
14. _________ angle is formed by combining two consecutive right angles.
15. Which of the following is obtuse angle in triangle ABC ?
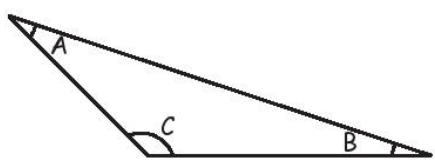
a) ∠A b) ∠B c) ∠C d) none of these
16. Hands of a clock at 2 hours shows _____ angle.
17. Which of the following alphabets has a right angle in it ?
a) L b) K c) Z d) N
18. Can a right-angled triangle have an obtuse angle?
True/False
19. An isosceles triangle can have a right-angled triangle. True/False

1. Answer :
35° ---> Acute angle
135° ---> Obtuse angle
205° ---> Reflex angle
180° ---> Straight angle
90° ---> Right angle
360° ---> Full angle
270° ---> Reflex angle
2. Answer :
Let a be the required angle.
4(a + 5) = 32
4a + 20 = 32
4a = 12
a = 3
Angle = 3°
Since 3° is less than 90°, the type of the angle is acute angle.
3. Answer :
Let b be the required angle.
2(3b + 20) = 1024
3b + 20 = 512
3b = 498
b = 166
Angle = 166°
Since 166° is greater than 90° but less than 180°, the type of the angle is obtuse angle.
4. Answer :
Let c be the required angle.
5c + 2 = 1222
5c = 1220
c = 244
Angle = 244°
Since 244° is greater than 180° but less than 360°, the type of the angle is reflex angle.
5. Answer :
Let d be the required angle.
5(d - 2) = 440
d - 2 = 88
d = 90
Angle = 90°
Since the angle is exactly 90°, the type of the angle is right angle.
6. Answer :
Let e be the required angle.
7(3e - 5) = 3745
3e - 5 = 535
3e = 540
e = 180
Angle = 180°
Since the angle is exactly 180°, the type of the angle is straight angle.
7. Answer :
Let f be the required angle.
2(9f - 15) = 6450
9f - 15 = 3225
9f = 3240
f = 360
Angle = 360°
Since the angle is exactly 360°, the type of the angle is full angle.
8. Answer :

The angle measure shown is lesser than 90 degree, then the given angle measure is acute angle.
9. Answer :

The angle measure shown is greater than 90 degree, then the given angle measure is obtuse angle.
10. Answer :

The shown angle measure is exactly 90 degree, then it is right angle.
11. Answer :
30° ==> Acute angle
45° ==> Acute angle
60°==> Acute angle
90° ==> Right angle
120°==> Obtuse angle
130° ==> Obtuse angle
170° ==> Obtuse angle
75° ==> Acute angle
12. Answer :
The angle which is greater than 0 and lesser than 90 degree, it is called acute angle.
13. Answer :
13. The angle which is greater than 90 and lesser than 180 degree, it is called obtuse angle.
14. Answer :
Sum of two right angles = 180 degree
Straight angle is formed by combining two consecutive right angles.
15. Answer :

a) ∠A = acute angle
b) ∠B = acute angle
c) ∠C = obtuse angle
So, answer is option c.
16. Answer :
The complete angle is 360 degree.
= 360/12
= 30
Angle between two consecutive numbers in the clock is 30 degree.
Angle between 12 and 2 is 60 degree, it is lesser than 90 degree.
Hands of a clock at 2 hours shows acute angle.
17. Answer :
Which of the following alphabets has a right angle in it ?
a) L b) K c) Z d) N
Option a, L creates right angle.
18. Answer :
Can a right-angled triangle have an obtuse angle?
Only one right angle will be there in any triangle, the other angles will be acute angle. So, the result is false.
True/False
19. Answer :
In any isosceles triangle, it can be a right-angled triangle. So, the answer is true.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation -
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37)


