TYPES OF TRIANGLES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Triangles can be broadly classified into two types.
1. Triangles based on the lengths of their sides.
2. Triangle based on their angles.
According to the lengths of their sides, triangles can be classified into three types.
1. Equilateral triangle
2. Isosceles triangle
3. Scalene triangle
Equilateral Triangle
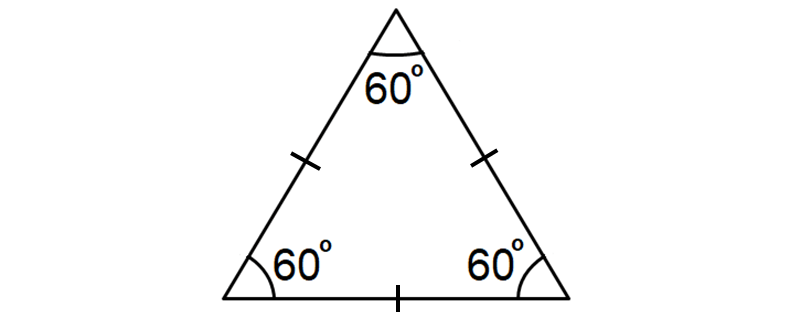
An equilateral triangle is a triangle in which all the three sides will be equal.
Each angle will be 60°.
Isosceles Triangle
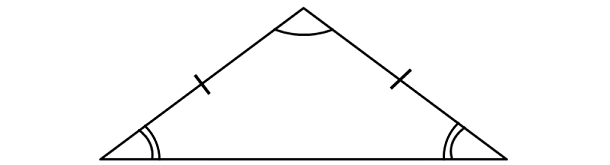
A triangle with two equal sides is called as isosceles triangle. The angles corresponding to the equal sides will always be equal.
Scalene Triangle
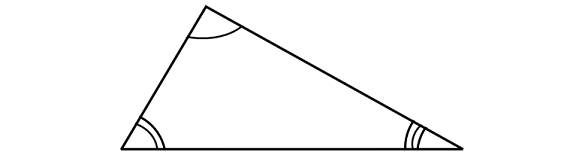
In a scalene triangle the length of all the three sides will be different. And also all the three angles will be different.
According to the interior angles, triangles can be classified into three types.
1. Right triangle
2. Acute triangle
3. Obtuse triangle
Acute Triangle
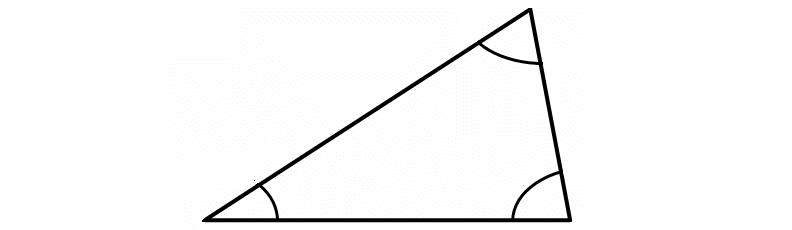
An acute triangle is a triangle with all three angles are less than 90°.
Right Triangle
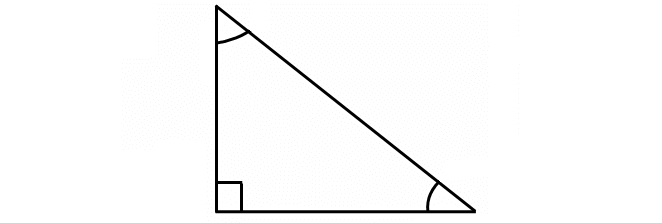
A right triangle is the triangle in which one of the angles is 90°.
Obtuse Triangle
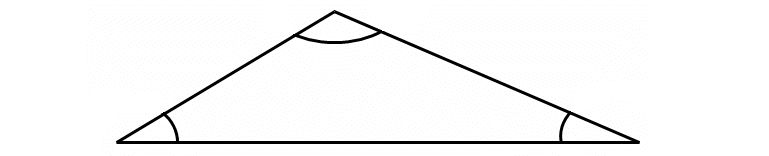
An obtuse triangle is a triangle in which one of the angles is obtuse (greater than 90°).
Solved Problems
Problem 1 :
Identify the type of triangle whose angles are 35°, 40°, 105°.
Solution :
(i) All the given three angles are different
(ii) One of the angles is greater than 90°
So, the given triangle is a scalene and obtuse triangle.
Problem 2 :
Identify the type of triangle whose angles are 55°, 65°, 60°.
Solution :
(i) All the given three angles are different
(ii) All the three angles are less than 90°
So, the given triangle is a scalene and acute triangle.
Problem 3 :
Identify the type of triangle whose angles are 50°, 40°, 90°.
Solution :
(i) All the given three angles are different
(ii) One of the angles is 90°
So, the given triangle is a scalene and right triangle.
Problem 4 :
Identify the type of triangle whose angles are 45°, 45°, 90°.
Solution :
(i) Two of the given angles are equal
(ii) One of the angles is 90°
So, the given triangle is an isosceles and right triangle.
Problem 5 :
Identify the type of triangle whose angles are 70°, 70°, 40°.
Solution :
(i) Two of the given angles are equal
(ii) All the three angles are less than 90°
So, the given triangle is an isosceles and acute triangle.
Problem 6 :
Identify the type of triangle whose angles are 30°, 30°, and 120°.
Solution :
(i) Two of the given angles are equal
(ii) One of the angles is greater than 90°
So, the given triangle is an isosceles and obtuse triangle.
Problem 7 :
Identify the type of triangle whose sides are 5 cm, 6 cm and 7 cm.
Solution :
The length of all the three sides are different.
So, the given triangle is a scalene triangle.
Problem 8 :
Identify the type of triangle whose sides are 6 cm, 6 cm and 8 cm.
Solution :
The lengths of two of the sides are equal.
So, the given triangle is an isosceles triangle.
Problem 9 :
If (3x + 3)° is one of the angles of an acute triangle, then find the value of x.
Solution :
Since the given triangle is acute triangle, all the three angles will be less than 90°.
So, (3x + 3)° will also be less than 90°.
(3x + 3)° < 90
3x < 87
x < 29
Problem 10:
If 50°, 40° and (2x + 4)°are the angles of a right triangle, then find the value of x.
Solution :
Since the given triangle is a right triangle, one of the angles must be 90°.
In the given three angles 50°, 40° and (2x+4)°, the first two angles are not right angles.
So the third angle (2x + 4)° must be right angle.
(2x + 4)° = 90°
2x + 4 = 90
2x = 86
x = 43
Problem 11 :
The sides of a triangle are 6cm, 8cm and 10cm. Check whether it is a right triangle.
Solution :
62 = 36, 82 = 64, 102 = 100
36 + 64 = 100
62 + 82 = 102
Sum of squares of two sides is equal to square of the third side.
The given sides satisfies Pythagorean Theorem. So the given triangle is a right triangle.
Problem 12 :
14. The sides of a triangle are 5in, 5in and 5√2in. Check whether it is a right triangle.
Solution :
52 = 25, 52 = 25, (5√2)2 = 50
25 + 25 = 50
52 + 52 = (5√2)2
Sum of squares of two sides is equal to square of the third side.
The given sides satisfies Pythagorean Theorem and also two of its sides are equal. So the given triangle is an isosceles right triangle.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 43)
Jan 04, 26 01:38 AM
10 Hard SAT Math Questions (Part - 43) -
90 Degree Clockwise Rotation
Jan 01, 26 06:58 AM
90 Degree Clockwise Rotation - Rule - Examples with step by step explanation -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Jan 01, 26 04:51 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations