CLASSIFY QUADRILATERALS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A closed geometric figure with four sides and four vertices is called a quadrilateral. The sum of all the four angles of a quadrilateral is 360°.
A quadrilateral can be classified as follows.
(i) Square
(ii) Rectangle
(iii) Parallelogram
(iv) Rhombus
(v) Isosceles Trapezoid
(vi) Kite
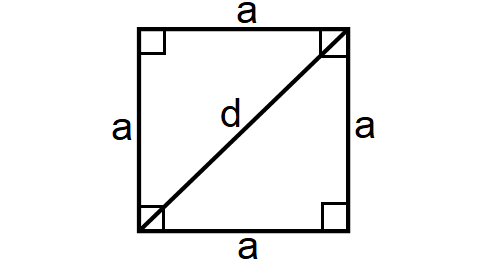
Square
A square is a regular quadrilateral, which means that it has four equal sides and four equal angles. It can also be defined as a rectangle in which two adjacent sides have equal length. A square with vertices ABCD would be denoted ABCD.
Properties :
1. All four sides of a square are same length, they are equal
2. Opposite side of a square are parallel
3. All four angles of a square are right angles
4. Sum of the angles of a square are equal to 360 degree.
5. Diagonals of a square are same length
6. Each diagonal of a square divides its into two equal symmetrical area.
7. Diagonals of a square intersect its right angles, and share each other half.
8. When the side length is given :
Area of a Square = a2
When the length of the diagonal is given :
Area of a Square = 1/2 ⋅ d2
Perimeter of a Square = 4a
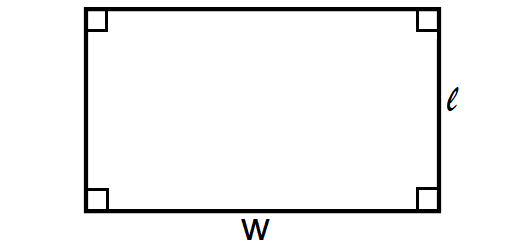
Rectangle
A rectangle is a quadrilateral with four right angles. It can also be defined as an equiangular quadrilateral, since equiangular means that all of its angles are equal.
Properties :
1. A pair of opposite sides of a rectangle are the same length, they are equal
2. A pair of opposite sides of a rectangle are parallel
3. An adjacent sides of a rectangle are always perpendicular
4. All four angles of a rectangles is right.
5. The sum all of the angles of a rectangle is equal to 360 degrees.
6. The diagonals of a rectangle are equal
7. The sum of squares two diagonals is equal to the sum of squares of the sides.
Area of a Rectangle = l ⋅ w
Perimeter of a Rectangle = 2(l + w)
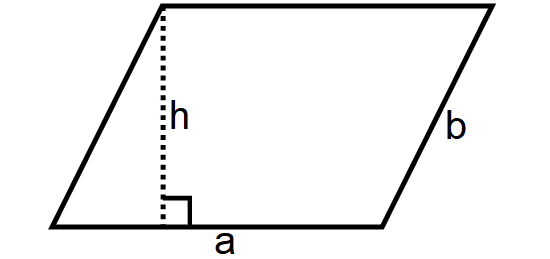
Parallelogram
A quadrilateral in which the opposite sides are parallel is called a parallelogram.
Properties :
1. Opposite sides are parallel and equal.
2. Opposite angles are equal and sum of any two adjacent angles is 180°.
3. Diagonals bisect each other.
4. The sum of the parallelogram angles is equal to 360 degrees.
5. Each diagonals divides the parallelogram into two equal triangle.
6. Two diagonals is divided parallelogram into two pairs of equal triangles.
Area of a Parallelogram = b ⋅ h
Perimeter of a Parallelogram = 2(a + b)
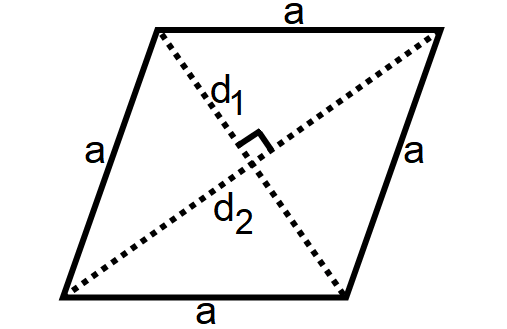
Rhombus
A rhombus is a simple quadrilateral whose four sides all have the same length.
Properties :
1. All sides are equal and opposite sides are parallel
2. Opposite angles are equal and sum of any two adjacent angles is 180°.
3. Diagonals bisect each other at right angles.
4. The intersecting point of the diagonals is the center of the symmetry.
5. Any rhombus can be inscribed a circle.
Area of a Rhombus = 1/2 ⋅ d1 ⋅ d2
Perimeter of a Rhombus = 4a
Isosceles Trapezoid
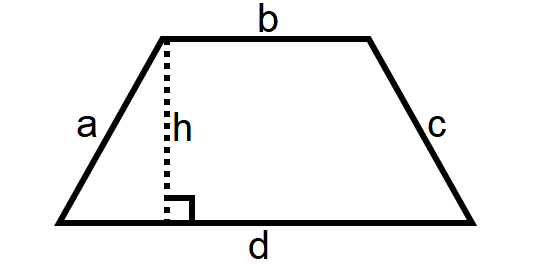
1. The legs are congruent by definition.
2. The bases are parallel by definition.
3. The lower base angles are congruent.
4. The upper base angles are congruent.
5. The diagonals are congruent.
6. Any lower base angle is supplementary to any upper base angle.
Area of a Trapezoid = 1/2 ⋅ h ⋅ (a + b)
Perimeter of a Trapezoid = a + b + c + d
Kite
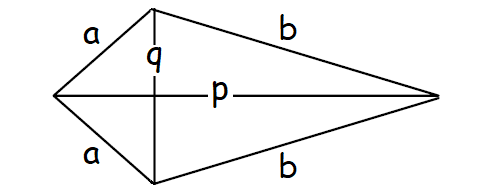
1. Two disjoint pairs of consecutive sides are congruent by definition.
2. The diagonals are perpendicular.
3. One diagonal is the perpendicular bisector of the other.
4. One of the diagonals bisects a pair of opposite angles.
5. One pair of opposite angles are congruent.
Area of a Kite = (p ⋅ q) / 2
Perimeter of a Trapezoid = 2a + 2b
Classify each quadrilateral with the name that best describes it.
Problem 1 :
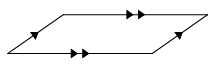
Solution :
From the figure given, the sides are parallel. So, it is parallelogram.
Problem 2 :
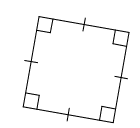
Solution :
All sides are equal. Each corner angles are 90 degree. Then it is square.
Problem 3 :
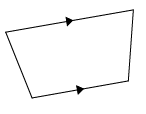
Solution :
One pair of sides are parallel and other pair of sides are non parallel. Then it is trapezium.
Problem 4 :
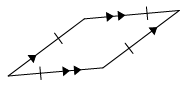
Solution :
Opposite sides are parallel, all four sides are congruent. Then it is rhombus.
Problem 5 :
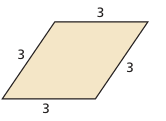
Solution :
Since all four sides are equal, then it is rhombus.
Problem 6 :
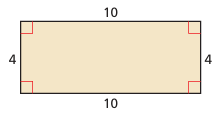
Solution :
Opposite sides are equal and each corner angles are 90 degree. Then it is a rectangle.
Problem 7 :
Find the measure of <A in quadrilateral BCDA if m<B = 60, m<C = 2x + 5, m<D = x and m<A = 2x + 5
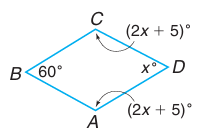
Solution :
Sum of interior angles of quadrilateral = 360
2x + 5 + 2x + 5 + x + 60 = 360
5x + 10 + 60 = 360
5x + 70 = 360
5x = 360 - 70
5x = 290
x = 290/5
x = 58
m<A = 2x + 5
= 2(58) + 5
= 116 + 5
= 121
So, m<A is 121 degree.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
90 Degree Clockwise Rotation
Jan 01, 26 06:58 AM
90 Degree Clockwise Rotation - Rule - Examples with step by step explanation -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Jan 01, 26 04:51 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations -
Solving the HARDEST SAT Math Questions ONLY using Desmos
Dec 31, 25 05:53 AM
Solving the HARDEST SAT Math Questions ONLY using Desmos
