CLASSIFICATION OF PAIR OF ANGLES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
We shall classify a pair of angles in the following way for better understanding and usages.
(i) Two angles that have the exact same measure are called congruent angles.
(ii) Two angles that have their measures adding to 90° are called complementary angles.
(iii) Two angles that have their measures adding to 180° are called supplementary angles.
(iv) Two angles between 0° and 360° are conjugate, if their sum equals 360°.
Example 1 :
In the figure shown below, let the lines l1 and l2 be parallel and t is transversal. Find the value of x.
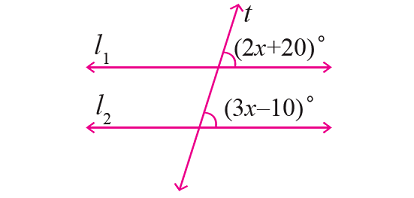
Solution :
From the given figure,
∠(2x + 20)° and ∠(3x - 10)° are corresponding angles.
So, they are congruent.
Then,
2x + 20 = 3x - 10
30 = x
Example 2 :
In the figure shown below, let the lines l1 and l2 be parallel and m is transversal. Identify the pairs of angles which are congruent.
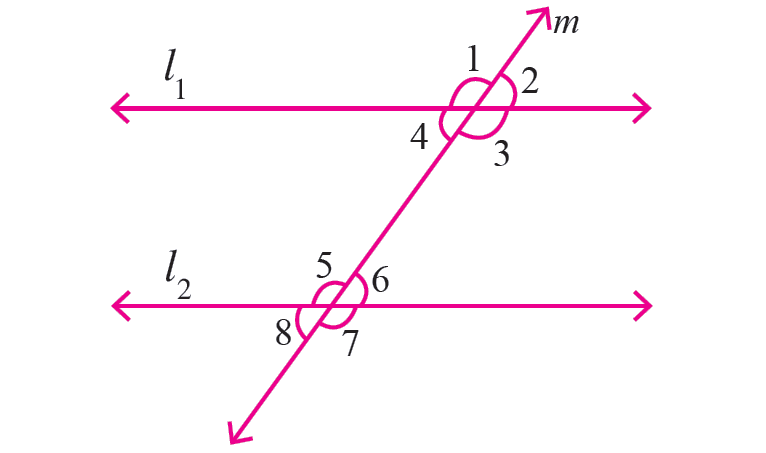
|
Vertically opposite angles are congruent. |
< 1 = < 3 < 2 = < 4 < 5 = < 7 < 6 = < 8 |
|
Corresponding angles are congruent. |
< 1 = < 5 < 2 = < 6 < 3 = < 7 < 4 = < 8 |
|
Alternate interior angles are equal. |
< 3 = < 5 < 4 = < 6 |
|
Alternate exterior angles are equal. |
< 1 = < 7 < 2 = < 8 |
Example 3 :
Find the value of x :
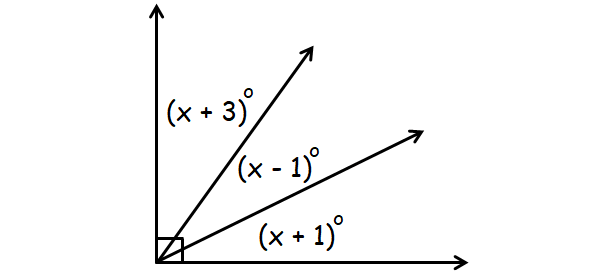
Solution :
From the picture above, it is clear that the angles (x+1), (x-1) and (x+3) are complementary.
Then,
(x+1) + (x-1) + (x+3) = 90
x + 1 + x - 1 + x + 3 = 90
Simplify.
3x + 3 = 90
Subtract 3 from each side.
3x = 87
Divide each side by 3.
x = 29
So, the value of x is 29.
Example 4 :
Find the value of x :
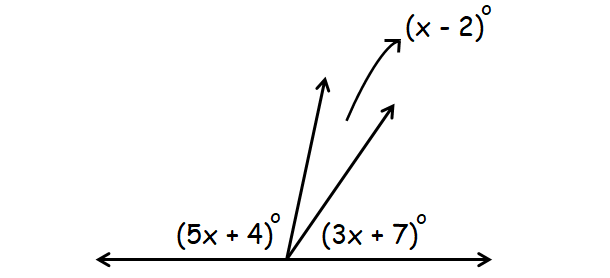
Solution :
From the picture above, it is clear (5x+4), (x-2) and (3x+7) are supplementary angles.
Then,
(5x+4) + (x-2) + (3x+7) = 180
5x + 4 + x -2 + 3x + 7 = 180
Simplify.
9x + 9 = 180
Subtract 9 from each side.
9x = 171
Divide each side by 9.
x = 19
So, the value of x is 19.
Example 5 :
Find the conjugate of the angle measure 97°.
Solution :
Let x° be the conjugate of the angle measure 97°.
Because x° and 97° are conjugate, their sum equals 360°.
Then,
x° + 97° = 360°
Subtract 97° from each side.
x° = 263°
So, the conjugate of the angle measure 97° is 263°.
Example 6 :
If (x + 30)° and (2x - 60)° are conjugate, find the value of x.
Solution :
Because (x + 30)° and (2x - 60)° are conjugate, their sum equals 360°.
Then,
(x + 30)° + (2x - 60)° = 360°
x + 30 + 2x - 60 = 360
Simplify.
3x - 30 = 360
Add 30 to each side.
3x = 390
Divide each side by 3.
x = 130
So, the value of x is 130.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
