CLASS 9 MATH WORKSHEET WITH SOLUTION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Solve the given equation below x + 2 log27 9 = 0
(A) -4/3 (B) 1/2 (C) 2/5
Solution :
x + 2log27 9 = 0
x = -2log27 9
x = log27 9-2
We know that,
If x = loga b then ax = b
27x = 9-2
(33)x = (32)-2
33x = 3-4
If bx = by then x = y
3x = -4
x = -4/3
So, the answer is -4/3.
Problem 2 :
In the given, ∠A = 64° , ∠ABC = 58°. If BO and CO are the bisectors of ∠ABC and ∠ACB respectively of ΔABC, find x° and y°
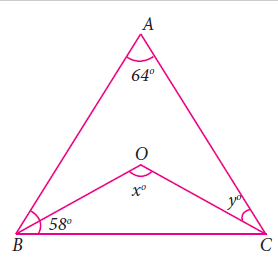
Solution :
Since BO and CO are bisectors of ABC and ACB.
<OBC = 58/2 = 29
In triangle ABC,
<ABC + <BAC + <BCA = 180
58 + 64 + <BCA = 180
<BCA = 180 - 122
<BCA = 58
<y = 58
In triangle OBC,
<OBC + <BOC + <BCO = 180
29 + <BOC + 29 = 180
<BOC = 180 - 58
x = <BOC = 122
Problem 3 :
Find the number of subsets for the set A = {1, 2, 3, 4, 5}
(A) 11 (B) 22 (C) 32
Solution :
Given, A = {1, 2, 3, 4, 5}
Here, A contains 5 elements.
So, n = 5
The number of subsets for A = 2n
= 25
= 32
So, the answer is 32.
Problem 4 :
{The number of engineering colleges in Singapore}
The above set is a --------
(A) singleton set (B) infinite set (C) finite set
Solution :
So, the answer is finite set.
Problem 5 :
The cardinal number of the set P {0}
(A) 3 (B) 4 (C) 1
Solution :
We know that,
The cardinal number of the set P {0} is n(P)
Here, P contains 1 element.
So, the n(P) is 1.
Problem 6 :
If A = {1, 2, 3} and B = {2, 3, 4}, find A n B.
(A) {1, 2, 3} (B) {2, 3} (C) {1, 2, 3, 4}
Solution :
Given, A = {1, 2, 3} and B = {2, 3, 4}
Find A n B.
The common elements in sets A and B is A n B = {2, 3}
So, the answer is {2, 3}
Problem 7 :
The equation x + 3y = 12, 3x + 9y = 24 has ------ solution.
(A) unique (B) infinite (C) no
Solution :
By writing the given equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 in the form, we get
x + 3y - 12 = 0
3x + 9y - 24 = 0
From the equations, let us find the values of a1, a2, b1, b2, c1, and c2
Here a1 = 1, b1 = 3 and c1 = -12
a2 = 3, b2 = 9 and c2 = -24
a1/a2 = 1/3 -----(1)
b1/b2 = 3/9 = 1/3 -----(2)
c1/c2 = 12/24 = 1/2 -----(3)
(1) = (2) ≠ (3)
Now, a1/a2 = b1/b2 ≠ c1/c2
So, it has no solution.
Problem 8 :
Solve 5x + 3y = 11, 3x + 5y = -3
(A) (1, 2) (B) (0, 3) (C) (4, -3)
Solution :
5x + 3y = 11 -----(1)
3x + 5y = -3 -----(2)
Using elimination method :
Subtract 3(1) - 5(2), we get
15x + 9y - 15x - 25y = 33 + 15
9y - 25y = 48
-16y = 48
y = -3
By applying y = -3 in equation (1), we get
5x + 3(-3) = 11
5x - 9 = 11
5x = 20
x = 4
So, the solution is (4, -3)
Problem 9 :
Find the sum of 2x4 - 3x2 + 5x + 3 and 4x + 6x3 - 6x2 - 1
(A) 2x4 + 6x3 - 9x2 + 9x + 2
(B) 4x4 + 6x3 - 9x2 - 9x
(C) -2x4 + 6x3 + 9x2 - 9x + 2
Solution :
By adding, we get
= 2x4 - 3x2 + 5x + 3 + 4x + 6x3 - 6x2 - 1
= 2x4 + 6x3 - 9x2 + 9x + 2
So, the answer is 2x4 + 6x3 - 9x2 + 9x + 2
Problem 10 :
If a/b = 5 then the value of (a - b)/(a + b) is
(A) 1/8 (B) 2/3 (C) 3/4
Solution :
Given, a/b = 5/1
Here a = 5 and b = 1
Then,
(a - b)/(a + b) = (5 - 1)/(5 + 1)
= 4/6
(a - b)/(a + b) = 2/3
So, the answer is 2/3.
Problem 11 :
Simplify (x2 - 9)/(2xy - 6y + 5x - 15)
Solution :
= (x2 - 9)/(2xy - 6y + 5x - 15) -----(1)
x2 - 32 = (x + 3)(x - 3)
2xy - 6y + 5x - 15 = 2y(x - 3) + 5(x - 3)
= (2y + 5)(x - 3)
By applying these values in (1), we get
= (x + 3)(x - 3) / (2y + 5)(x - 3)
= (x + 3) / (2y + 5)
Problem 12 :
ABCDEFGH is cuboid with a square base of side x cm. CG = 20 cm and AG = 28 cm. Calculate the value of x.
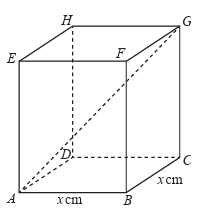
Solution :
In the square which is at the base ABCD,
the side length = x cm
Using Pythagorean theorem,
AC2 = AB2 + BC2
AC2 = x2 + x2
AC2 = 2x2
AC = √2x2
AC = x√2
In the cube,
AG2 = AC2 + CG2
282 = 2x2 + (20)2
524 = 2x2 + 400
2x2 = 524 - 400
2x2 = 124
x2 = 62
x = √62
x = 7.87 cm
So, side length of cube is 7.87 cm.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 50)
Mar 06, 26 07:48 PM
Digital SAT Math Problems and Solutions (Part - 50) -
Digital SAT Math Problems and Solutions (Part - 49)
Mar 06, 26 06:47 PM
Digital SAT Math Problems and Solutions (Part - 49) -
Digital SAT Math Problems and Solutions (Part - 48)
Mar 06, 26 05:24 PM
Digital SAT Math Problems and Solutions (Part - 48)


