CIRCUMFERENCE AND ARC LENGTH WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Find the circumference of a circle with radius 6 centimeters. Round decimal answers to two decimal places.
Problem 2 :
Find the radius of a circle with circumference 31 meters. Round decimal answers to two decimal places.
Problem 3 :
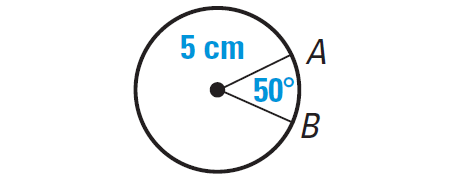
Find the length of the arc AB in the diagram shown below.
Problem 4 :
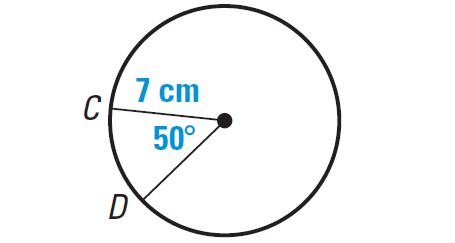
Find the length of the arc CD in the diagram shown below.
Problem 5 :
The track shown below has six lanes. Each lane is 1.25 meters wide. There is a 180° arc at each end of the track. The radii for the arcs in the first two lanes are given.
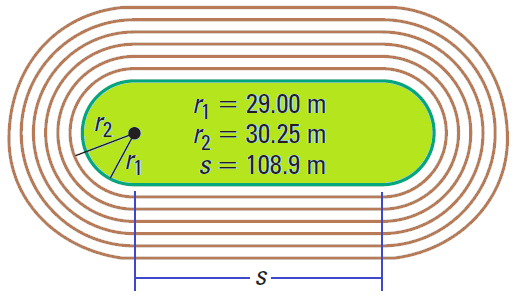
a. Find the distance around Lane 1.
b. Find the distance around Lane 2.
Problem 6 :
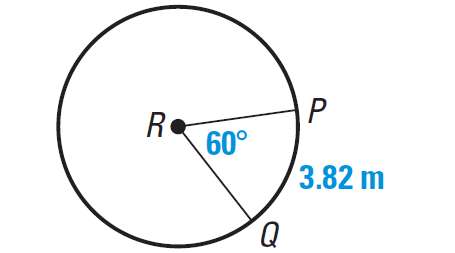
Find the circumference of the circle shown below.
Problem 7 :
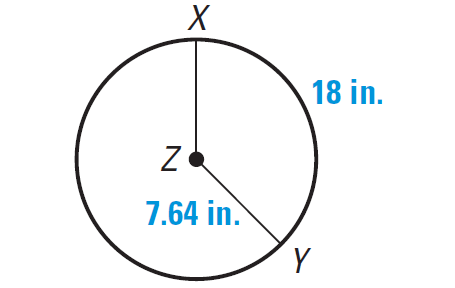
Find the m∠arc XY.
Problem 8 :
Tires from two different automobiles are shown below. How many revolutions does each tire make while traveling 100 feet ? Round decimal answers to one decimal place.


Answers
Problem 1 :
Find the circumference of a circle with radius 6 centimeters. Round decimal answers to two decimal places.
Answer :
The formula for circumference of a circle is given by
C = 2πr
Substitute r = 6.
C = 2π(6)
C = 12π
Use calculator to get the value of π.
C ≈ 37.70
Hence, the circumference is about 37.70 centimeters.
Problem 2 :
Find the radius of a circle with circumference 31 meters. Round decimal answers to two decimal places.
Answer :
The formula for circumference of a circle is given by
C = 2πr
Substitute C = 31.
31 = 2πr
Divide each side by 2π.
31/2π = r
Use calculator to get the value of π.
4.93 ≈ r
Hence, the radius is about 4.93 meters.
Problem 3 :
Find the length of the arc AB in the diagram shown below.

Answer :
Formula for length of the arc :
Arc length of AB = [m∠arc AB/360°] ⋅ 2πr
Substitute.
Arc length of AB = [50°/360°] ⋅ 2π(5)
Simplify.
Arc length of AB ≈ 4.36 centimeters
Problem 4 :
Find the length of the arc CD in the diagram shown below.

Answer :
Formula for length of the arc :
Arc length of CD = [m∠arc CD/360°] ⋅ 2πr
Substitute.
Arc length of CD = [50°/360°] ⋅ 2π(7)
Simplify.
Arc length of AB ≈ 6.11 centimeters
Problem 5 :
The track shown below has six lanes. Each lane is 1.25 meters wide. There is a 180° arc at each end of the track. The radii for the arcs in the first two lanes are given.

a. Find the distance around Lane 1.
b. Find the distance around Lane 2.
Answer :
The track is made up of two semicircles and two straight sections with length s.To find the total distance around each lane, find the sum of the lengths of each part.Round decimal answers to one decimal place.
|
Part (a) : Distance = 2s + 2πr1 = 2(108.9) + 2π(29.00) ≈ 400.0 meters |
Part (b) : Distance = 2s + 2πr2 = 2(108.9) + 2π(30.25) ≈ 407.9 meters |
Problem 6 :
Find the circumference of the circle shown below.

Answer :
(Arc length of PQ)/2πr = m∠arc PQ/360°
3.82/2πr = 60°/360°
3.82/2πr = 1/6
Take reciprocal on each side.
2πr/3.82 = 6/1
2πr/3.82 = 6
Multiply each side by 3.82
2πr = 6(3.82)
2πr = 6(3.82)
2πr = 22.92
Hence, the circumference of the circle is about 22.92 meters.
Problem 7 :
Find the m∠arc XY.

Answer :
(Arc length of XY)/2πr = m∠arc XY/360°
Substitute.
18/2π(7.64) = m∠arc XY/360°
18/15.28π = m∠arc XY/360°
Multiply each side by 360°.
360° ⋅ 18/2π(7.64) = m∠arc XY
135° ≈ m∠arc XY
Hence, m∠arc XY is about 135°.
Problem 8 :
Tires from two different automobiles are shown below. How many revolutions does each tire make while traveling 100 feet?Round decimal answers to one decimal place.

Answer :
Tire A has a diameter of 14 + 2(5.1), or 24.2 inches. Its circumference is π(24.2), or about 76.03 inches.
Tire B has a diameter of 15 + 2(5.25), or 25.5 inches. Its circumference isπ(25.5), or about 80.11 inches.
Divide the distance traveled by the tire circumference to find the number of revolutions made.
First convert 100 feet to 1200 inches.
|
Tyre A : = 100 ft/76.03 in = 1200 in/76.03 in ≈ 15.8 revolutions |
Tyre B : = 100 ft/80.11 in = 1200 in/80.11 in ≈ 15.0 revolutions |
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
Specifying Units of Measure
Dec 15, 25 07:09 PM
Specifying Units of Measure -
Quantitative Reasoning Questions and Answers
Dec 14, 25 06:42 AM
Quantitative Reasoning Questions and Answers -
Coin Tossing Probability
Dec 13, 25 10:11 AM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems