CIRCUMCENTER OF A TRIANGLE

The point of concurrency of the perpendicular bisectors of the sides of a triangle is called the circumcenter of the triangle.

The following steps will be useful to find circumcenter of a triangle. 

Step 1 : 

Find the equations of the perpendicular bisectors of any two sides of the triangle. 

Step 2 : 

Solve the two equations found in step 2 for x and y. 

The solution (x, y) is the circumcenter of the triangle given.

Example : 

Find the co ordinates of the circumcenter of a triangle whose vertices are (2, -3), (8, -2) and (8, 6).

Solution : 

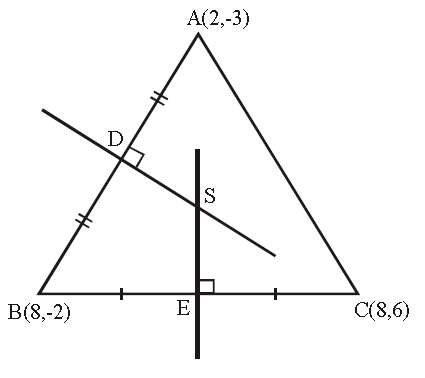
Let A(2, -3), B(8, -2) and C(8, 6) be the vertices of the triangle. 

D is the midpoint of AB and E is the midpoint of BC. 

Midpoint of AB is

=  [(x₁ + x₂)/2, (y₁ + y₂)/2]

Substitute (x₁, y₁)  =  (2, -3) and (x₂, y₂)  =  (8, -2).

=  [(2 + 8)/2, (-3 - 2)/2]

=  [10/2, -5/2]

=  (5, -5/2)

So, the point D is (5, -5/2). 

Slope of AB is 

=  [(y₂ - y₁)/(x₂ - x₁)]

Substitute (x₁, y₁)  =  (2, -3) and (x₂, y₂)  =  (8, -2).

=  [(-2 - (-3)] / (8 - 2)

=  (-2 + 3) / 6

=  1/6

Slope of the perpendicular line to AB is

=  -1 / slope of AB

=  -1 / (1/6)

=  -1 ⋅ (6/1)

=  -6

Equation of the perpendicular bisector to the side AB :

y  =  mx + b

Substitute  m  =  -6. 

y  =  -6x + b -----(1)

Substitute the point D(5, -5/2) for (x, y) into the above equation. 

-5/2  =  -6(5) + b

-2.5  =  -30 + b

Add 30 to each side. 

27.5  =  b

Substitute b  =  27.5 in (1). 

(1)-----> y  =  -6x + 27.5

Equation of the perpendicular line through D is 

y  =  -6x + 27.5 -----(2)

Midpoint of BC is

=  [(x₁ + x₂)/2, (y₁ + y₂)/2]

Substitute (x₁, y₁)  =  (8, -2) and (x₂, y₂)  =  (8, 6).

=  [(8 + 8)/2, (-2 + 6)/2]

=  [16/2, 4/2]

=  (8, 2)

So, the point E is (8, 2). 

Slope of BC is 

=  [(y₂ - y₁)/(x₂ - x₁)]

Substitute (x₁, y₁)  =  (8, -2) and (x₂, y₂)  =  (8, 6).

=  [6 - (-2)] / (8 - 8)

=  (6 + 2) / 0

=  8/0

Slope of the perpendicular line to BC is

=  -1 / slope of BC

=  -1 / (8/0)

=  -1 ⋅ (0/8)

=  -1 ⋅ 0

=  0

Equation of the perpendicular bisector to the side BC :

y  =  mx + b

Substitute  m  =  0. 

y  =  b -----(3)

Substitute the point E(8, 2) for (x, y) into the above equation. 

2  =  b

Substitute b  =  2 in (1). 

(1)-----> y  =  2

Equation of the perpendicular line through D is 

y  =  2 -----(4)

Solving (2) and (4), we get

x  =  4.25  and  y  =  2

Therefore, the circumcenter of the triangle ABC is 

(4.25, 2)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.