CHECK WHETHER THE GIVEN POLYNOMIAL IS FACTOR OF ANOTHER POLYNOMIAL USING LONG DIVISION

(1) Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following

(i) p(x) = x³ – 3 x² + 5 x – 3     g (x) = x² - 2         

(ii) p(x) = x⁴ – 3 x² + 4 x + 5     g (x) = x² + 1 -x       

(iii) p(x) = x⁴ – 5 x + 6     g (x) = 2 - x²         

(2) Check whether the first polynomial is a factor of second polynomial by dividing the second polynomial by the first polynomial

(i) t² – 3 , 2 t⁴ + 3 t³ – 2 t² – 9 t – 12

(ii)  x² + 3 x + 1     g (x) = 3 x⁴ + 5 x ³ – 7 x² + 2 x + 2  

(iii)  x³ - 3 x + 1     g (x) = x⁵ -4 x³ + x² + 3 x + 1          

(3)  Obtain all other zeroes of 3 x⁴ + 6 x³ – 2 x² – 10 x – 5, if two of its zeroes are √(5/3) and -√(5/3)

(4) On dividing x³ – 3 x² + x + 2 by the polynomial g(x), the quotient and remainder were (x – 2) and – 2x + 4. Find g(x)

Question 1 :

(i) p(x) = x³ – 3 x² + 5 x – 3     g (x) = x² - 2

Solution :

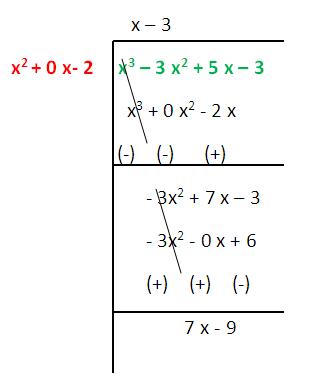
Quotient = x - 3

Remainder = 7 x - 9

(ii) p(x) = x⁴ – 3 x² + 4 x + 5     g (x) = x² + 1 - x

Solution :

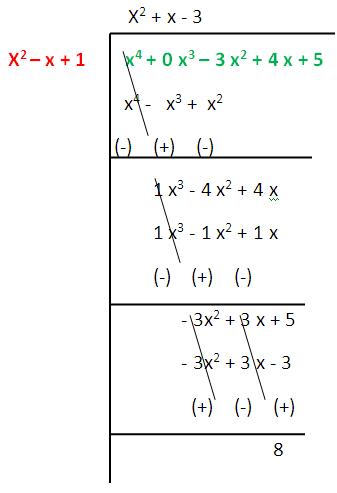
Quotient = x² + x - 3

Remainder = 8

(iii) p(x) = x⁴ – 5 x + 6     g (x) = 2 - x²   

Solution :

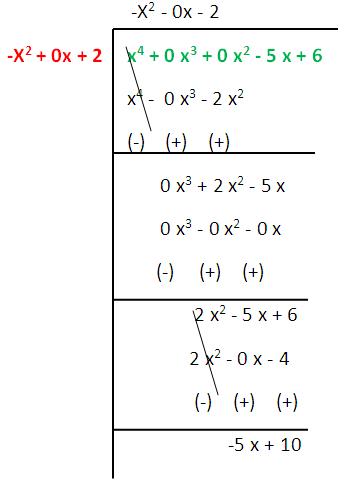
Quotient = -x² - 2

Remainder = -5 x + 10

Question 2 :

Check whether the first polynomial is a factor of second polynomial by dividing the second polynomial by the first polynomial

(i) t² – 3 , 2 t⁴ + 3 t³ – 2 t² – 9 t – 12

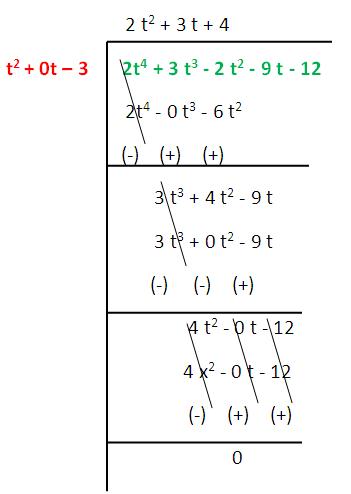
Since the remainder is 0, we say that the given polynomial is a factor of other polynomial.

(ii)  x² + 3 x + 1     g (x) = 3 x⁴ + 5 x ³ – 7 x² + 2 x + 2     

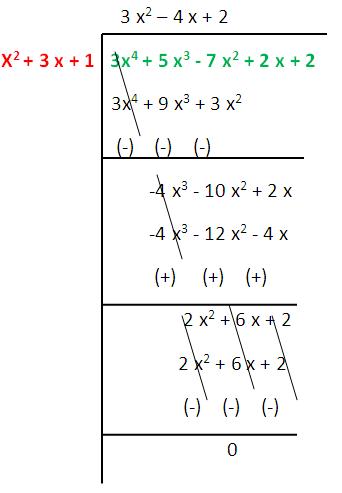
The remainder is zero. So, we say that the first polynomial is the factor of second polynomial.

(iii)  x³ - 3 x + 1     g (x) = x⁵ -4 x³ + x² + 3 x + 1    

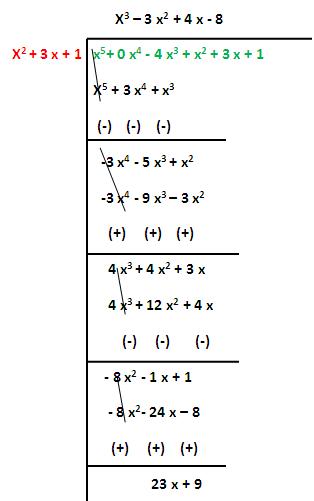
The first polynomial is not a factor of second polynomial.

Question 3 :

Obtain all other zeroes of 3 x⁴ + 6 x³ – 2 x² – 10 x – 5, if two of its zeroes are √(5/3) and -√(5/3)

Solution :

Since the highest power of the given polynomial is 4, there will be four zeroes for the given polynomial. 

Out of the four zeroes, we have two zeroes. By combining these two factors, we will get a quadratic equation. By dividing the given polynomial by this quadratic equation, we will get quotient as quadratic equation.

By solving the quadratic equation that we find quotient, we will get two more zeroes.

x = √(5/3)   x = -√(5/3) 

(x - √(5/3)) (x + √(5/3)) = (x² – 5/3)

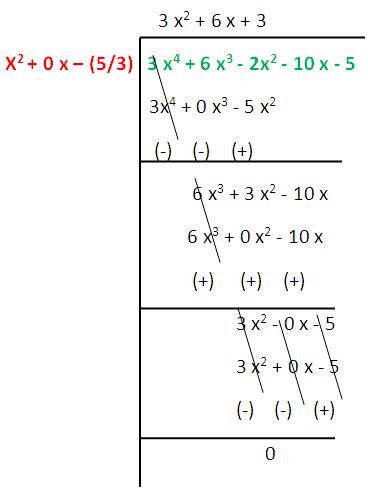
3 x² + 6 x + 3  =  3 x² + 3 x + 3 x + 3

                        =  3x (x + 1) + 3 (x + 1)

                        =  (3x + 3) (x + 1)

Question 4 :

On dividing x³ – 3 x² + x + 2 by the polynomial g(x), the quotient and remainder were (x – 2) and – 2x + 4. Find g(x)

Solution :

Division algorithm

P (x) = g (x) x q (x) + r (x)

P (x) = x³ – 3 x² + x + 2

q (x) = (x – 2)

r (x) = - 2x + 4

   x³ – 3 x²+ x + 2 = g (x) x (x – 2) + (- 2x + 4)

   x³ – 3 x² + x + 2 + 2 x - 4 = g (x) x (x – 2)

   x³ – 3 x² + 3 x - 2 = g (x) x (x – 2)

   (x³ – 3 x² + 3 x – 2)/(x - 2) = g (x)

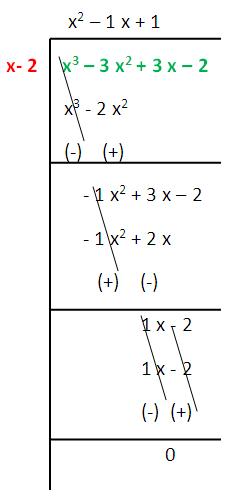
Hence, g (x) = x² – 1 x + 1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.