CHECK IF THE GIVEN ANGLE IN STANDARD POSITION

Example 1 : 

Is the following angle, θ, in standard position ?

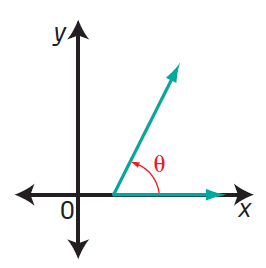
Solution :

In the picture given above the angle is not in the standard position. 

Explanation :

The vertex of initial arm and terminal arm is not at origin.

Example 2 : 

Is the following angle, θ, in standard position ?

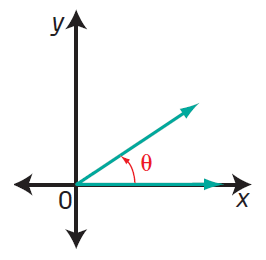
Solution :

In the picture given above the angle is in the standard position. 

Explanation :

The vertex is at origin and initial arm is in x axis. Hence the given angle is in standard position.

Example 3 : 

Is the following angle, θ, in standard position ?

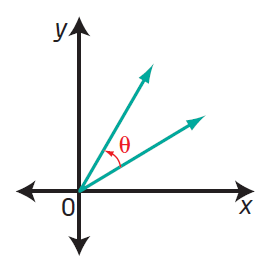
Solution :

In the picture given above the angle is not in the standard position. 

Explanation :

The initial arm is not on the x-axis.

Example 4 :

Is the following angle, θ, in standard position ?

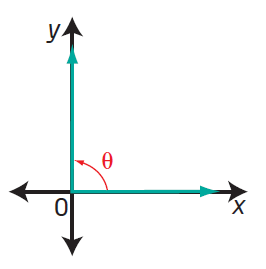
Solution :

In the picture given above the angle is in the standard position. 

Explanation :

The vertex is at origin and initial arm is in x axis. Hence the given angle is in standard position.

Example 5 :

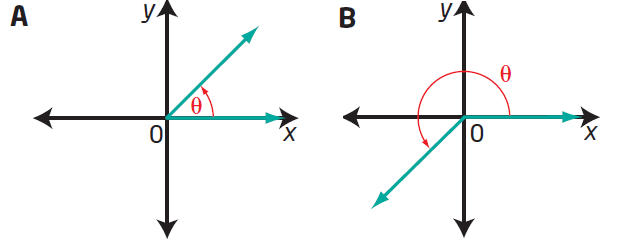
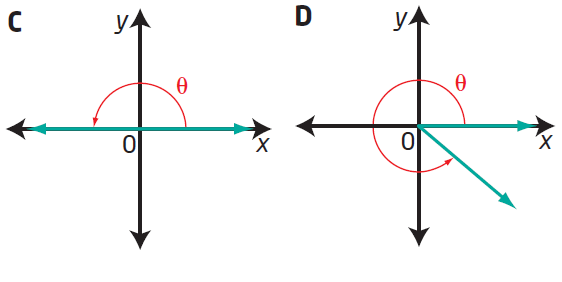
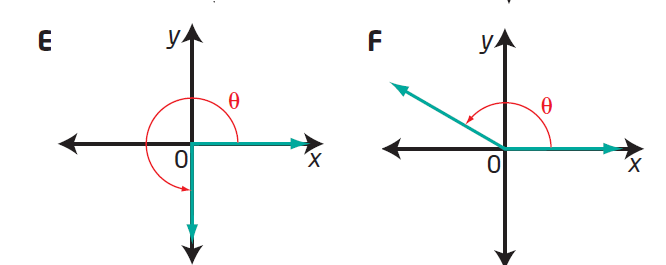
Without measuring, match each angle with a diagram of the angle in standard position.

(a) 150°     (b) 180°      (c) 45°     (d) 320°

(e) 215°     (f) 270°

Solution :

(a)  150 

It is greater than 90 but lesser than 180.The picture F represents angle 150.

(b)  Picture C represents 180 degree.

(c)  45

45 degree is greater than 0 but lesser than 90. Picture A represents 45 degree.

(d)  320

320 degree is greater than 270 and lesser than 360. Picture D represents 320 degree.

(e)  215

215 is greater than 180 but lesser than 270, picture B represents 215.

(f)  270

Picture F represents 270 degree.

Example 6 :

Draw the angle with the given measure in standard position.

1)   −340°        2)   150°       3)   −185°

4)  300°          5)  −340°

Solution :

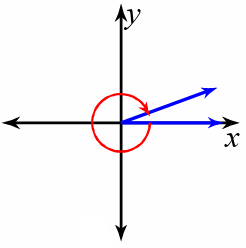
1)  −340° 

Since it is negative angle measure, we have to go clockwise direction of rotation. The angle measure lies between -270 to -360, so the terminal arm should lie in the fourth quadrant.

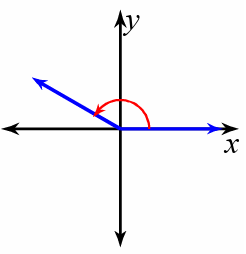
2)   150°

Since it is positive angle measure, we have to go for counter clockwise rotation. The given angle measure lies between 90 degree to 180 degree. Then the terminal arm will lie in the second quadrant.

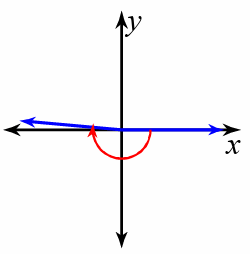
3)   −185°

Since it is negative angle measure, we have to go for clockwise rotation. The given angle measure lies between 180 degree to 270 degree. Then the terminal arm will lie in the second quadrant.

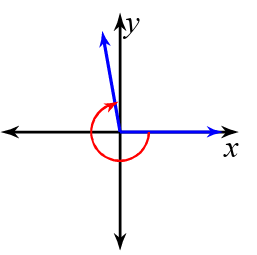
4)  300° 

Since it is positive angle measure, we have to go for counter clockwise rotation. The given angle measure lies between 270 degree to 360 degree. Then the terminal arm will lie in the fourth quadrant.

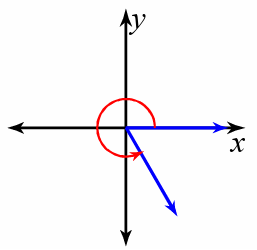
5)   −340°

Since it is negative angle measure, we have to go for clockwise rotation. The given angle measure lies between -270 degree to -360 degree. Then the terminal arm will lie in the first quadrant.

Example 7 :

Find the measure of each principal angle.

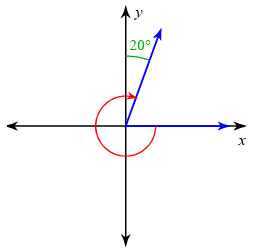
Solution :

The terminal side lies in the first quadrant, the initial arm is rotating in clockwise direction, the angle measure shown is 20 degree.

Principal angle = -270 - 20

= -290 degree

Example 8 :

Find the measure of each principal angle.

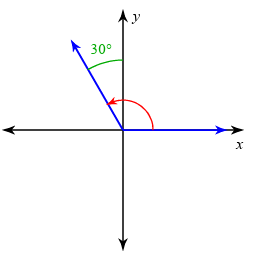
Solution :

The terminal side lies in the second quadrant, the initial arm is rotating in counter clockwise direction, the angle measure shown is 30 degree.

Principal angle = 90 + 30

= 120 degree

Example 9 :

Find the measure of each principal angle.

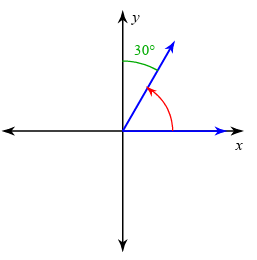
Solution :

The terminal side lies in the first quadrant, the initial arm is rotating in counter clockwise direction, the angle measure shown is 30 degree. The angle measure shown must be a positive angle measure.

Principal angle = 90 - 30

= 60 degree

Example 10 :

Find the measure of each principal angle.

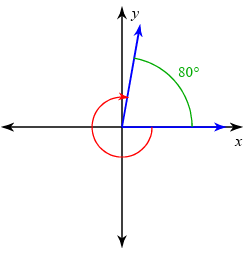
Solution :

The terminal side lies in the first quadrant, the initial arm is rotating in clockwise direction, the angle measure shown is 30 degree. The shown angle measure must be a negative angle.

Principal angle = -360 + 80

= -280 degree

Example 11 :

State the quadrant in which the terminal side of each angle lies.

1) 300°    2) 170°    3) 235°     4) −229°

Solution :

1) 300°

The given angle measure lies between 270 degree to 360 degree, then the terminal arm should lie in the third quadrant.

2) 170°

The given angle measure lies between

90 degree to 180 degree, then the terminal arm should lie in the second quadrant.

3) 235°

The given angle measure lies between 180 degree to 270 degree, then the terminal arm should lie in the third quadrant.

4) −229°

The given angle measure lies between -180 degree to -270 degree, then the terminal arm should lie in the third quadrant.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.