CENTRAL ANGLES AND ARC MEASURES WORKSHEET

Assume that lines which appear to be diameters are actual diameters.

Problem 1 :

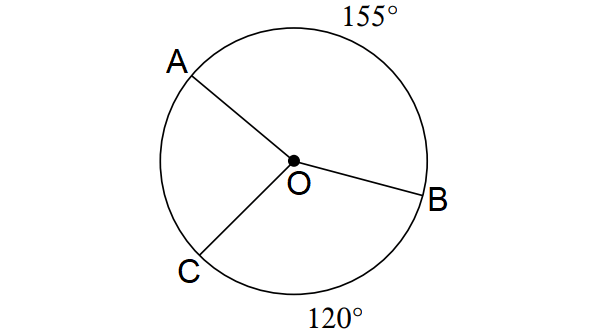
In the diagram shown above, find m∠AOC.

Solution :

In the circle above,

m∠arc AB + m∠arc BC + m∠arc CA = 360°

155° + 120° + m∠arc CA = 360°

275° + m∠arc CA = 360°

m∠arc CA = 85°

m∠AOC = 85°

Problem 2 :

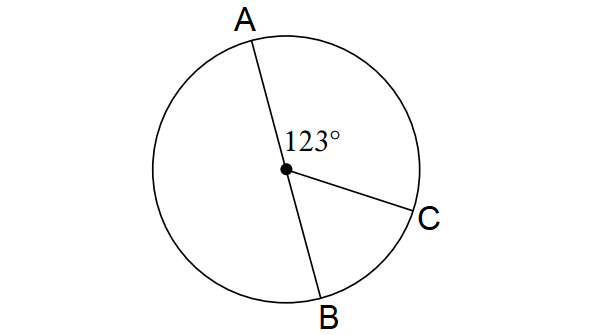
In the diagram shown above, find the following arc measures. 

(i) m∠arc BC

(ii) m∠arc ABC

Solution :

(i) m∠arc BC :

AB is the diameter of the above circle. 

m∠arc AB = 180°

m∠arc BC + m∠arc CA = 180°

m∠arc BC + 123° = 180°

m∠arc BC = 57°

(ii) m∠arc ABC :

m∠arc ABC = m∠arc AB + m∠arc BC

= 180° + 57°

= 237°

Problem 3 :

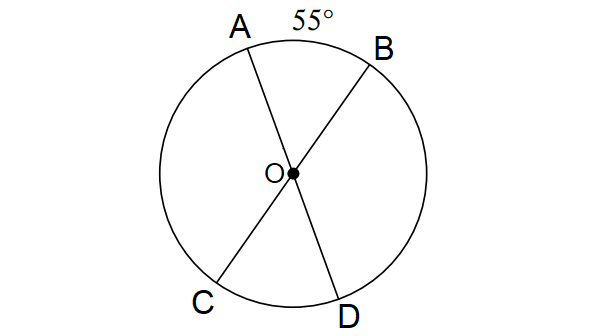
In the diagram shown above, find the following measures. 

(i) m∠arc CD

(ii) m∠AOC

(iii) m∠arc BD

(iv) m∠arc ABC

(v) m∠arc CBD

(i) m∠arc CD :

Solution :

i)  m∠AOB and m∠COD are vertical angles. 

m∠COD = m∠AOB

m∠arc CD = m∠arc AB

m∠arc CD = 55°

(ii) m∠AOC :

BC is the diameter of the above circle. 

m∠arc BAC = 180°

m∠arc BA + m∠arc AC = 180°.

55° + m∠arc AC = 180°.

m∠arc AC = 125°.

m∠AOC = 125°.

(iii) m∠arc BD : 

m∠BOD and m∠AOC are vertical angles. 

m∠BOD = m∠AOC

m∠BOD = 125°

m∠arc BD = 125°

(iv) m∠arc ABC : 

m∠arc ABC = m∠arc ABD + m∠arc DC

= 180° + 55°

= 235°

(v) m∠arc CBD : 

m∠arc CBD = m∠arc CAB + m∠arc BD

= 180° + 125°

= 305°

Problem 4 :

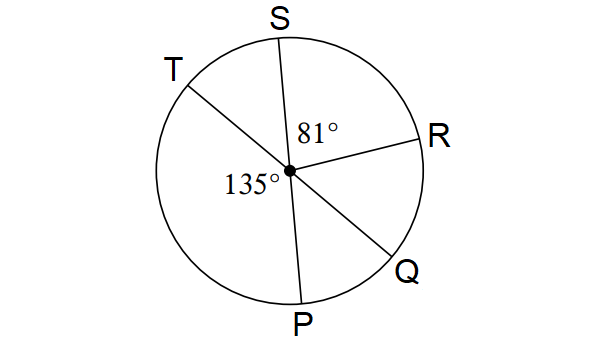
Solution :

In the diagram shown above, find the  m∠arc QTR.

Find m∠arc QP :

PS is the diameter of the above circle.

m∠arc PTS = 180°

m∠arc PT + m∠arc TS = 180°

135° + m∠arc TS = 180°

m∠arc TS = 45°

Find m∠arc QTR :

m∠QTR = m∠arc QT + m∠arc TS + m∠arc SR

= 180° + 45° + 81°

= 306°

Problem 5 :

Solution :

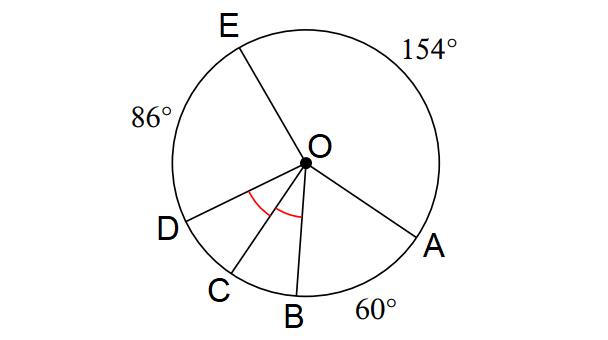
In the diagram shown above, find the following measures. 

m∠BOD, m∠BOE and m∠BOC

Find m∠BOD :

In the circle above,

m∠arc AB + m∠arc BCD + m∠arc DE + m∠arc EA = 360°

60° + m∠arc BCD + 86° + 154° = 360°

m∠arc BCD + 300° = 360°

m∠arc BCD = 60°

m∠BOD = 60°

Find m∠BOE :

m∠BOE = m∠arc BCD + m∠arc DE

= 60° + 86°

= 146°

Find m∠BOC :

In the above diagram, m∠BOC = m∠COD.

m∠BOC + m∠COD = m∠BOD

m∠BOC + m∠BOC = m∠BOD

2m∠BOC = 60°

m∠BOC = 30°

Problem 6 :

Solution :

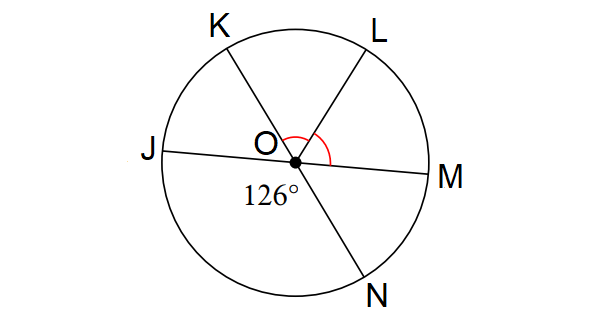
In the diagram shown above, find the following measures. 

m∠KOL and m∠arc MNK

In the diagram above, m∠JON and ∠KOM are vertical angles.

m∠KOM = m∠KOM

m∠KOM = 126°

m∠KOL + m∠LOM = 126°

In the above diagram, m∠KOL = m∠LOM.

m∠KOL + m∠KOL = 126°

2m∠KOL = 126°

m∠KOL = 63°

Find m∠arc MNK :

m∠arc MNK = 360° - m∠arc KLM

m∠arc MNK = 360° - m∠KOM

m∠arc MNK = 360° - 126°

m∠arc MNK = 234°

Problem 7 :

Find the value of x in the diagram shown below.

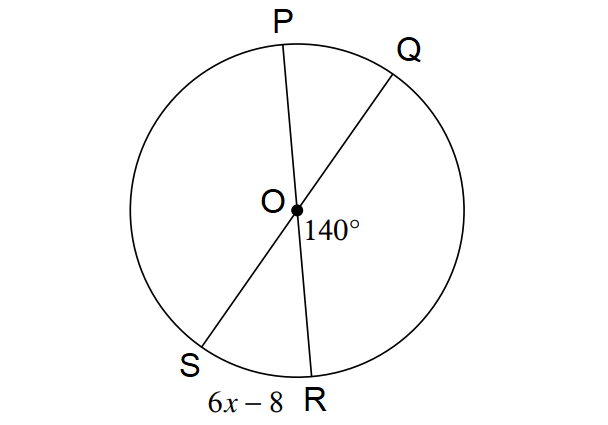
Solution :

In the circle above, PR is the diameter.

m∠arc PQR = 180°

m∠POQ + m∠QOR = 180°

m∠POQ + 140° = 180°

m∠POQ = 40°

In the diagram above, m∠SOR and m∠POQ are vertical angles.

m∠SOR = m∠POQ

6x - 8 = 40

6x = 48

x = 8

Problem 8 :

Find the value of x in the diagram shown below.

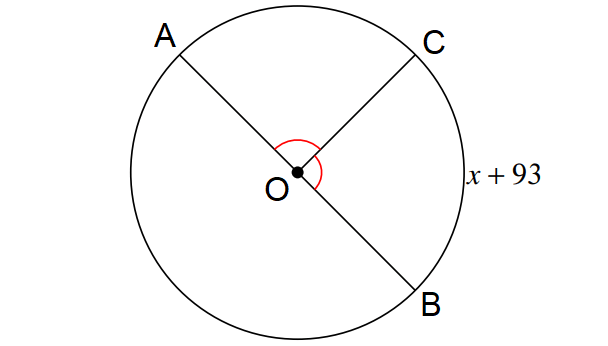
Solution :

In the circle above, AB is the diameter.

m∠AOC + m∠COB = 180°

In the diagram above, m∠AOC = m∠COB.

m∠COB + m∠COB = 180°

2m∠COB = 180°

m∠COB = 90°

x + 93 = 90

x = -3

Problem 9 :

Find the value of x in the diagram shown below.

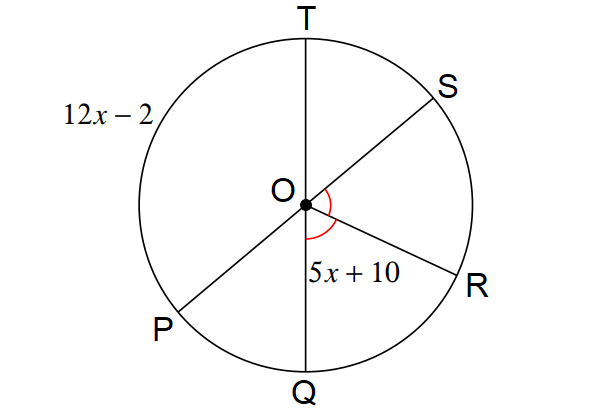
Solution :

In the diagram above, m∠POT and m∠QOS are vertical angles.

m∠POT = m∠QOS

m∠POT = m∠QOR + m∠ROS

In the diagram above, m∠QOR = m∠ROS.

m∠POT = m∠QOR + m∠QOR

m∠POT = 2m∠QOR

12x - 2 = 2(5x + 10)

12x - 2 = 10x + 20

2x = 22

x = 11

Problem 10 :

Find the value of x in the diagram shown below.

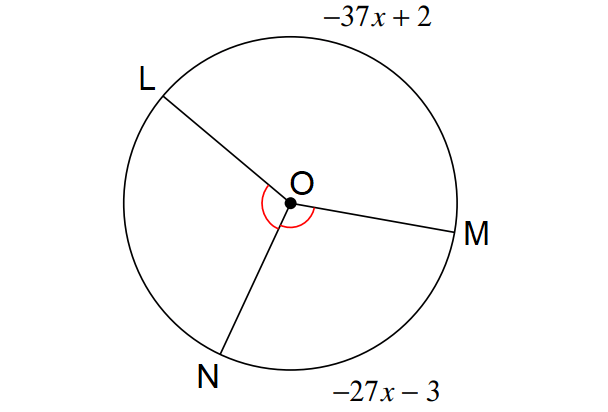
Solution :

In the circle above,

m∠arc LM + m∠arc MN + m∠arc NL = 360°

In the diagram above, m∠arc MN = m∠arc NL.

m∠arc LM + m∠arc MN + m∠arc MN = 360°

m∠arc LM + 2m∠arc MN = 360°

-37x + 2 + 2(-27x - 3) = 360

-37x + 2 - 54x - 6 = 360

-91x - 4 = 360

-91x = 364

x = -4

Find the measure of the arc or central angle indicated. Assume that lines which appear to be diameters are actual diameters.

Problem 11 :

measure of arc WV

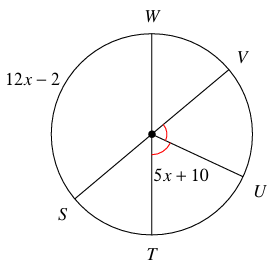
Solution :

Measure of arc WS = 12x - 2

Measure of arc TU = measure of arc UV = 5x + 10

Measure of arc WS = measure of TV

12x - 2 = 5x + 10 + 5x + 10

12x - 2 = 10x + 10

12x - 10x = 10 + 2

2x = 12

x = 12/2

x = 6

So, the value of x is 2.

Problem 12 :

<VST 

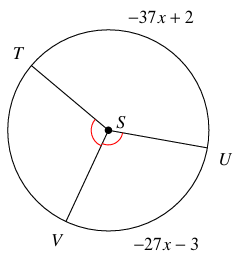
Solution :

Measure of arc TV + measure of arc VU + measure of arc TU = 360

Here measure of arc TV = measure of arc VU = -27x - 3

-37x + 2 + 2(-27x - 3) = 360

-37x + 2 - 54x - 6 = 360

-91x - 4 = 360

-91x = 364

x = -364/91

x = -4

So, the value of x is -4.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.