HOW TO FIND THE CENTER AND RADIUS OF A CIRCLE FROM ITS EQUATION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Equation of a circle in standard form with center (0, 0) and radius 'r'.
x2 + y2 = r2
Equation of a circle in standard form with center (h, k) and radius 'r'.
(x - h)2 + (y - k)2 = r2
Equation of a circle in general form :
x2 + y2 + 2gx + 2fy + c = 0
where the center is (-g, if) and radius is √(g2 + f2 - c).
Find the center and radius of the following circles.
Example 1 :
x2 + y2 = 25
Solution :
The given equation of the circle is in the form of
x2 + y2 = r2
So, the center of the given circle is (0, 0).
Radius :.
r2 = 25
r = 5 units
Example 2 :
(x - 1)2 + (y - 3)2 = 9
Solution :
The given equation of the circle is in the form of
(x - h)2 + (y - k)2 = r2
Center :
(h, k) = (0, 0)
Radius :.
r2 = 9
r = 3 units
Example 3 :
(x + 3)2 + (y - 5)2 = 15
Solution :
The given equation of the circle is in the form of
(x - h)2 + (y - k)2 = r2
Center :
(h, k) = (-3, 5)
Radius :.
r2 = 15
r = √15 units
Example 4 :
x2 + y2 - 4x - 6y + 9 = 0
Solution :
The given equation of circle is in general form.
Comparing
x2 + y2 - 4x - 6y + 9 = 0
and
x2 + y2 + 2gx + 2fy + c = 0
we get
2g = -4 ----> g = -2 ----> -g = 2
2f = -6 ----> f = -3 ----> -f = 3
Center :
(-g, -f) = (2, 3)
Radius :
r = √(g2 + f2 - c)
= √(4 + 9 - 9)
= √4
= 2 units
Example 5 :
Find the center of the circle described on the line joining the points (1, 2) and (2, 4) as its diameter.
Solution :
Center of the circle = Midpoint of the diameter
Substitute (x1, y1) = (1, 2) and (x2, y2) = (2, 4).
(1 + 2)/2, (2 + 4)/2
= 3/2, 6/2
= (1.5, 3) is the center of the circle.
Example 6 :
The equation of a circle C, with center O is
(x - 3)2 + (y + 2)2 = 25
a) Find the coordinates of the center O.
b) Find the radius of C.
c) Show that the point (6, 2) lies on C.
Solution :
(x - 3)2 + (y + 2)2 = 25
a)
By comparing this equation with
(x - h)2 + (y - k)2 = r2
(x - 3)2 + (y - (-2))2 = 52
center is (h, k) ==> (3, -2)
b) radius = 5
c) Applying the point (6, 2) in the equation of circle, we get
(6 - 3)2 + (2 + 2)2 = 25
32 + 42 = 25
9 + 16 = 25
25 = 25
So, the point (6, 2) lies in the circle.
Example 7 :
A circle has center (5, 2) and radius 4.
(a) Write down the equation of the circle.
(b) Does the point (7, 4) lie on the circle?
Solution :
Center (5, 2) and radius = 4
Equation of circle :
(x - h)2 + (y - k)2 = r2
(x - 5)2 + (y - 2)2 = 42
x2 - 10x + 25 + y2 - 4y + 4 = 16
x2 + y2 - 10x - 4y + 4 - 16 = 0
x2 + y2 - 10x - 4y - 12 = 0
Example 8 :
Find the equation of the circle
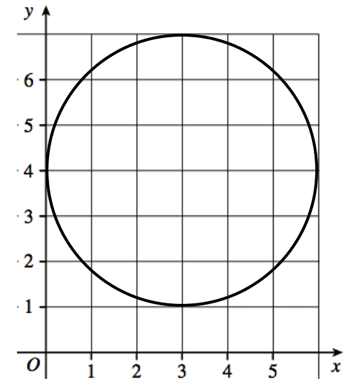
Solution :
From the circle shown, center of the circle is (3, 4)
Distance between (0, 4) and (3, 4)
= √(x2 - x1)2 + (y2 - y1)2
= √(4 - 4)2 + (3 - 0)2
= √02 + 32
= 3
Radius of the circle = 3 units.
Equation of circle :
(x - h)2 + (y - k)2 = r2
(x - 3)2 + (y - 4)2 = 32
x2 - 6x + 9 + y2 - 8y + 16 = 9
x2 + y2 - 6x - 8y + 16 - 9 = 0
x2 + y2 - 6x - 8y + 7 = 0
Example 9 :
A circle C has centre O The points A (0, 6) and B (8, 6) lie on the diameter of C.
(a) Find the coordinates of the centre O.
(b) Write down the equation of the circle.
Solution :
Endpoints of the diameter are A (0, 6) and B (8, 6)
a)
Midpoint of diameter = center of the circle
= (x1 + x2)/2, (y1 + y2)/2
= (0 + 8)/2, (6 + 6)/2
= 8/2, 12/2
Center of the circle = O (4, 6)
Distance between center and one endpoint of the diameter
= √(x2 - x1)2 + (y2 - y1)2
O (4, 6) and A (0, 6)
= √(x2 - x1)2 + (y2 - y1)2
= √(4 - 0)2 + (6 - 6)2
= √42 + 02
radius = 4
b)
Equation of circle :
(x - 4)2 + (y - 6)2 = 42
x2 - 8x + 16 + y2 - 12y + 36 - 16 = 0
x2 + y2 - 8x - 12y + 16 + 36 - 16 = 0
x2 + y2 - 8x - 12y + 36 = 0
Example 10 :
AB is a diameter of a circle C. O is the centre of the circle A has coordinates (-2, 12) and B has coordinates (8, 2).
(a) Find the centre of the circle, O.
(b) Find the equation of C
(c) Show the point D, (10, 8) lies on C.
Solution :
a) Midpoint of diameter = center of the circle
= (x1 + x2)/2, (y1 + y2)/2
A(-2, 12) and B(8, 2)
= (-2 + 8)/2, (12 + 2)/2
= 6/2, 14/2
Center = O (3, 7)
Distance between center and one endpoint of the diameter
= √(x2 - x1)2 + (y2 - y1)2
O (3, 7) and A (-2, 12)
= √(x2 - x1)2 + (y2 - y1)2
= √(-2 - 3)2 + (12 - 7)2
= √(-5)2 + 52
= √(25 + 25)
= √50
Radius = 5√2
b)
Equation of circle :
(x - 3)2 + (y - 7)2 = √502
x2 - 6x + 9 + y2 - 14y + 49 = 50
x2 + y2 - 6x - 14y + 58 - 50 = 0
x2 + y2 - 6x - 14y + 8 = 0
c) (x - 3)2 + (y - 7)2 = √502
Applying (10, 8), we get
(10 - 3)2 + (8 - 7)2 = √502
72 + 12 = 50
49 + 1 = 50
50 = 50
So, the point lies on the circle.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
ASTC Formula in Trigonometry
Dec 23, 25 11:34 PM
ASTC Formula in Trigonometry - Concepts - Examples and Solved Problems -
Coin Tossing Probability
Dec 23, 25 11:29 PM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems -
Permutation and Combination
Dec 23, 25 11:28 PM
Permutation and Combination - Definition - Formulas - Shortcuts - Difference between permutation and combination
