CARDINALITY OF SETS

Cardinality of a set is a measure of the number of elements in the set. 

For example, let A  =  { -2, 0, 3, 7, 9, 11, 13 }

Here, n(A) stands for cardinality of the set A

And n (A)  =  7

That is, there are 7 elements in the given set A. 

In case, two or more sets are combined using operations on sets, we can find the cardinality using the formulas given below.

Formula 1 :

n(A u B)  =  n(A) + n(B) - n(A n B)

If A and B are disjoint sets, n(A n B)  =  0

Then, n(A u B)  =  n(A) + n(B) 

Formula 2 : 

n(A u B u C)  =  n(A) + n(B) + n(C) - n(A n B) - n(B n C)                                  - n(A n C) + n(A n B n C)

If A, B and C are all disjoint sets, 

n(A n B)  = 0, n(B n C)  =  0, n(A n C)  =  0, n(A n B n C)  =  0

Then, n(A u B)  =  n(A) + n(B) + n(C)

Addition Theorem on Sets

Theorem 1 : 

n(AuB)  =  n(A) + n(B) - n(AnB)

Theorem 2 : 

n(AuBuC) : 

= n(A) + n(B) + n(C) - n(AnB) - n(BnC) - n(AnC) + n(AnBnC)

Explanation : 

Let us come to know about the following terms in details.

n(AuB)  =  Total number of elements related to any of the two events A & B.

n(AuBuC)  =  Total number of elements related to any of the three events A, B & C. 

n(A)  =  Total number of elements related to  A.

n(B)  =  Total number of elements related to  B.

n(C)  =  Total number of elements related to  C.

For  three events A, B & C, we have 

n(A) - [n(AnB) + n(AnC) - n(AnBnC)] : 

Total number of elements related to A only.

n(B) - [n(AnB) + n(BnC) - n(AnBnC)] :

Total number of elements related to B only.

n(C) - [n(BnC) + n(AnC) + n(AnBnC)] :

Total number of elements related to C only.

n(AnB) :

Total number of elements related to both A & B

n(AnB) - n(AnBnC) : 

Total number of elements related to both (A & B) only.

n(BnC) : 

Total number of elements related to both B & C

n(BnC) - n(AnBnC) :

Total number of elements related to both (B & C) only.

n(AnC) :

Total number of elements related to both A & C

n(AnC) - n(AnBnC) :

Total number of elements related to both (A & C) only.

For  two events A & B, we have

n(A) - n(AnB) :

Total number of elements related to A only.

n(B) - n(AnB) :

Total number of elements related to B only.

Understanding Word Problem

In a group of students, 65 play foot ball, 45 play hockey, 42 play cricket, 20 play foot ball and hockey, 25 play foot ball and cricket, 15 play hockey and cricket and 8 play all the three games. 

Let F, H and C represent the set of students who play foot ball, hockey and cricket respectively.

Venn diagram related to the above situation :

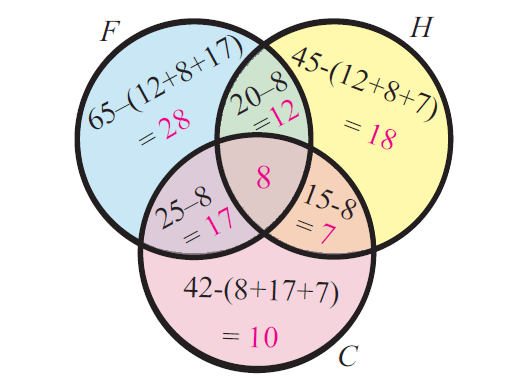
From the venn diagram, we can have the following details.

No. of students who play foot ball = 65

No. of students who play foot ball only = 28

No. of students who play hockey = 45

No. of students who play hockey only = 18

No. of students who play cricket = 42

No. of students who play cricket only = 10

No. of students who play both foot ball &  hockey = 20

No. of students who play both (foot ball & hockey) only = 12

No. of students who play both hockey & cricket = 15

No. of students who play both (hockey & cricket) only = 7

No. of students who play both foot ball and cricket = 25

No. of students who play both (foot ball and cricket) only = 17

No. of students who play all the three games = 8

Solving Word Problem

In a group of students, 65 play foot ball, 45 play hockey, 42 play cricket, 20 play foot ball and hockey, 25 play foot ball and cricket, 15 play hockey and cricket and 8 play all the three games. Find the total number of students in the group (Assume that each student in the group plays at least one game).

Step 1 :

Let F, H and C represent the set of students who play foot ball, hockey and cricket respectively.

Step 2 :

From the given information, we have

n(F)  =  65 , n(H)  =  45, n(C)  =  42,

n(FnH)  =  20, n(FnC)  =  25, n(HnC)  =  15

n(FnHnC)  =  8

Step 3 :

From the basic stuff, we have

Total number of students in the group is n(FuHuC). 

n(FuHuC) is equal to 

=  n(F) + n(H) + n(C) - n(FnH) - n(FnC) - n(HnC) + n(FnHnC)

Then, we have

n(FuHuC)  =  65 + 45 + 42 -20 - 25 - 15 + 8

n(FuHuC)  =  100

So, the total number of students in the group is 100.

Alternative Method (Using venn diagram) :

Step 1 :

Venn diagram related to the information given in the question :

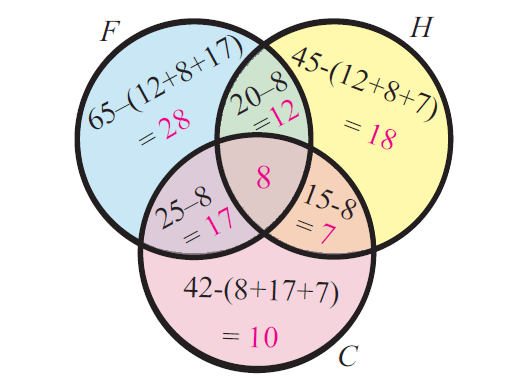
Step 2 :

Total number of students in the group :

=  28 + 12 + 18 + 7 + 10 + 17 + 8

=  100

So, the total number of students in the group is 100.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.