CALCULATING MARKUPS AND MARKDOWNS

A markup is one kind of percent increase. We can use a bar model to represent the retail price of an item, that is, the total price including the markup.

An example of a percent decrease is a discount, or markdown. A price after a markdown may be called a sale price. We can also use a bar model to represent the price of an item including the markdown.

Mark up ----> Increasing

To get profit in a business, a trader increases the cost price and sells the product. This increment in price is called as "Mark up"  

This "Mark up can either be in percent or in dollars. 

Mark Down ----> Decreasing

To increase the sale, stores will decrease the price of a product by giving offer or discount. This offer or discount is called as "Mark down". 

This mark down can either be in percent or in dollars. 

Hints

Hint 1 :

Cost price and marked up percentage are given.

Cost price  =  C.P,  Marked up percentage  =  m%

Then,

Selling price (S.P)  =  (100 + m)% ⋅ C.P

Hint 2 :

List price and marked down percentage are given.

List price  =  L.P, Marked down percentage  =  m%

Then,

Selling price (S.P)  =  (100 - m)% ⋅ L.P

Hint 3 :

List price price and marked down value (in dollars ) are given. 

List price  =  L.P, Marked down value  =  $m

Then,

mark down rate  =  (m / L.P) ⋅ 100%

Hint 4 :

Cost price and marked up value are given

Cost price  =  C.P, Marked up value  =  $m

Then,

mark up rate  =  (m / C.P) ⋅ 100% 

Hint 5 :

Cost price and selling price are given. 

Cost price  =  C.P, Selling price  =  S.P and S.P > C.P

So, Gain  =  S.P - C.P 

Then,

mark up rate  =  (Gain / C.P) ⋅ 100%

Hint 6 :

Selling price and profit percentage are given. 

How to find cost price ? 

Use hint 1 and solve for C.P

Hint 7 :

Selling price and loss percentage are given. 

How to find cost price ? 

Use hint 2 and solve for C.P

Hint 8 :

Marked price : It is the price before discount given. 

Selling price  =  Marked price - Discount value

Hint 9 :

Marked price  =  M.P, Discount percentage  =  D%

Then, the discount value is

=  D% ⋅ M.P

Selling price is 

=  (100 - D)% ⋅ M.P

Hint 10 :

Marked price (M.P) and discount value are given. 

Then the discount percentage is 

=  (Discount value / M.P) ⋅ 100% 

Hint 11 :

Retailer using false weight : 

A trader cheats his customer to make a profit by stating that he sells at cost price. But he gives his customer less than 1000 grams (false weight) for every 1 kilogram. 

Then, the profit percentage is 

=  (Cheated value /  False weight) ⋅ 100 %

Here,

Cheated value  =  Original weight - False weight

Hint 12 :

Two articles are sold at the same price. But, one is sold at a profit of p% and other one is sold at a loss of p%. 

Then, the net result of the transaction is loss. 

The loss percentage is 

=  (p² / 100)%

Hint 13 :

The cost price of two articles is same. But, one is sold at a profit of p% and other one is sold at a loss of p%. 

Then, the net result of the transaction is no profit and no loss. 

Examples

Example 1 : 

To make a profit, stores mark up the prices on the items they sell. A sports store buys skateboards from a supplier for s dollars. What is the retail price for skateboards that the manager buys for $35 and $56 after a 42% markup ?

Solution : 

Step 1 : 

Use a bar model.

Draw a bar for the cost of the skateboard S.

Then draw a bar that shows the markup: 42% of S, or 0.42S.

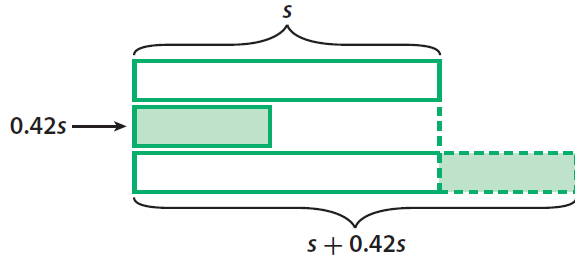
These bars together represent the cost plus the markup.

That is

S + 0.42S

Step 2 :

Retail price = Original cost + Markup

= S + 0.42S

= 1S + 0.42S

= 1.42S

Step 3 : 

Use the expression to find the retail price of each skateboard.

S  =  $35 ----> Retail price  =  1.42($35)  =  $49.70

S  =  $56 ----> Retail price  =  1.42($56)  =  $79.52

Example 2 : 

A discount store marks down all of its holiday merchandise by 20% off the regular selling price. Find the discounted price of decorations that regularly sell for $16 and $23.

Solution : 

Step 1 : 

Use a bar model.

Draw a bar for the regular price P.

Then draw a bar that shows the discount: 20% of P, or 0.2P.

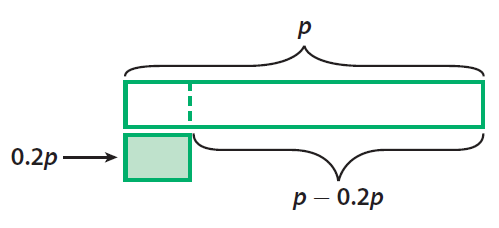
The difference between these two bars represents the price minus the discount.

That is,

P - 0.2P

Step 2 :

Sale price  =  Original price - Markdown

=  p - 0.2p

=  1p - 0.2p

=  0.8p

Step 3 :

Use the expression to find the sale price of each decoration.

p  =  $16 --->  Sale price  =  0.8($16)  =  $12.80

p  =  $23 --->  Sale price  =  0.8($23)  =  $18.40

Example 3 : 

On selling 20 units of an item, the profit is equal to cost price of 5 units. Find the mark mark up rate.  

Solution :

Let m be the cost price of one unit. 

Then, we have

Cost price of 5 units  =  5m

Cost price of 20 units  =  20m

Given : On selling 20 units of an item, the profit is equal to cost price of 5 units.

Then, we have

Profit  on selling 20 units  =  C.P of 5 units  =  5m 

Mark up rate  =  (profit / cost) ⋅ 100%

Mark up rate  =  (5m / 20m) ⋅ 100%

Mark up rate  =  (1 / 4) ⋅ 100%

Mark up rate  =  25%

Example 4 :

Difference between the cost price of two products is $10. Difference between the selling price is $20. If one is sold at 20% profit and other one is sold at 20% loss, find the cost price of each product.  

Solution :

Let x and y be the cost prices of two products. 

Then, we have

x - y  =  10 -----(1)

Let us assume that x is sold at 20% profit.

Then, the selling price of x is

=  120% ⋅ x

=  1.2x

Let us assume that y is sold at 20% loss. 

Then, the selling price of y is

=  80% ⋅ y

=  0.8y

Given : Difference between the selling price is $20

1.2x - 0.8y  =  20

Multiply each side by 10.

12x - 8y  =  200

Divide each side by 4.

3x - 2y  =  50 -----(2)

Solving (1) and (2), we get

x  =  30

y  =  20 

So, the cost prices of the two products are $30 and $20.

Example 5 : 

A trader marks his goods 20% above the cost price and allows a discount of 10% for cash. Find the mark up rate.

Solution :

Let the cost price be $100. 

Then, marked price  is $120.

Let x be the selling price. 

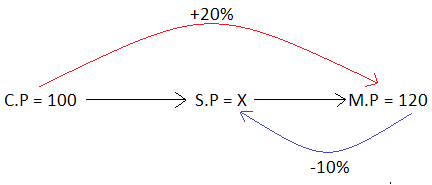
From the above picture, we get

90% of (M.P)  =  x

(0.9) ⋅ 120  =  x

108  =  x

Therefore, the selling price is $108.

Cost price  =  $100

Selling Price  =  $108

Mark up rate  =  8%

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.