CALCULATING MARKUPS AND MARKDOWNS WORKSHEET

1) To make a profit, stores mark up the prices on the items they sell. A sports store buys skateboards from a supplier for s dollars. What is the retail price for skateboards that the manager buys for $35 and $56 after a 42% markup ?

2) A discount store marks down all of its holiday merchandise by 20% off the regular selling price. Find the discounted price of decorations that regularly sell for $16 and $23.

3) On selling 20 units of an item, the profit is equal to cost price of 5 units. Find the mark mark up rate.  

4) Difference between the cost price of two products is $10. Difference between the selling price is $20. If one is sold at 20% profit and other one is sold at 20% loss, find the cost price of each product.  

5) A trader marks his goods 20% above the cost price and allows a discount of 10% for cash. Find the mark up rate.

Detailed Answer Key

Answer (1) : 

Step 1 : 

Use a bar model.

Draw a bar for the cost of the skateboard S.

Then draw a bar that shows the markup: 42% of S, or 0.42S.

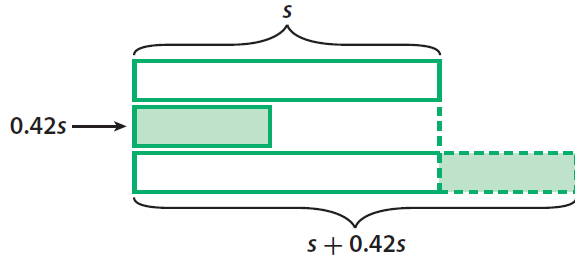
These bars together represent the cost plus the markup.

That is

S + 0.42S

Step 2 :

Retail price = Original cost + Markup

= S + 0.42S

= 1S + 0.42S

= 1.42S

Step 3 : 

Use the expression to find the retail price of each skateboard.

S  =  $35 ----> Retail price  =  1.42($35)  =  $49.70

S  =  $56 ----> Retail price  =  1.42($56)  =  $79.52

Answer (2) : 

Step 1 : 

Use a bar model.

Draw a bar for the regular price P.

Then draw a bar that shows the discount: 20% of P, or 0.2P.

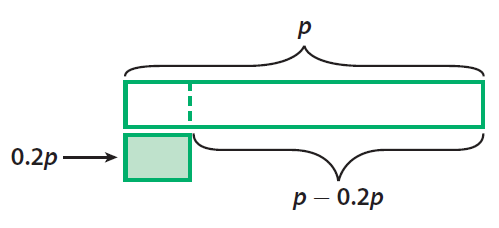
The difference between these two bars represents the price minus the discount.

That is,

P - 0.2P

Step 2 :

Sale price  =  Original price - Markdown

=  p - 0.2p

=  1p - 0.2p

=  0.8p

Step 3 :

Use the expression to find the sale price of each decoration.

p  =  $16 --->  Sale price  =  0.8($16)  =  $12.80

p  =  $23 --->  Sale price  =  0.8($23)  =  $18.40

Answer (3) :

Let m be the cost price of one unit. 

Then, we have

Cost price of 5 units  =  5m

Cost price of 20 units  =  20m

Given : On selling 20 units of an item, the profit is equal to cost price of 5 units.

Then, we have

Profit  on selling 20 units  =  C.P of 5 units  =  5m 

Mark up rate  =  (profit / cost) ⋅ 100%

Mark up rate  =  (5m / 20m) ⋅ 100%

Mark up rate  =  (1 / 4) ⋅ 100%

Mark up rate  =  25%

Answer (4) :

Let x and y be the cost prices of two products. 

Then, we have

x - y  =  10 -----(1)

Let us assume that x is sold at 20% profit.

Then, the selling price of x is

=  120% ⋅ x

=  1.2x

Let us assume that y is sold at 20% loss. 

Then, the selling price of y is

=  80% ⋅ y

=  0.8y

Given : Difference between the selling price is $20

1.2x - 0.8y  =  20

Multiply each side by 10.

12x - 8y  =  200

Divide each side by 4.

3x - 2y  =  50 -----(2)

Solving (1) and (2), we get

x  =  30

y  =  20 

So, the cost prices of the two products are $30 and $20.

Answer (5) :

Let the cost price be $100. 

Then, marked price  is $120.

Let x be the selling price. 

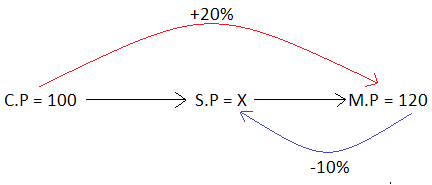
From the above picture, we get

90% of (M.P)  =  x

(0.9) ⋅ 120  =  x

108  =  x

Therefore, the selling price is $108.

Cost price  =  $100

Selling Price  =  $108

Mark up rate  =  8%

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.