BOX PLOT WORKSHEET

Problem 1 :

Make a box-plot for the data given below. 

4.3,  5.1,  3.9,  4.5,  4.4,  4.9,  5.0,  4.7,  4.1,  4.6,  4.4,  4.3, 4.8,  4.4,  4.2,  4.5,  4.4

Problem 2 :

The heights of several students are shown. 

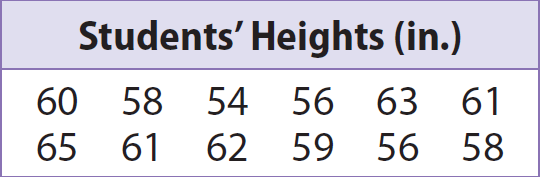
(i) Make a box-plot for the data.

(ii) What percent of the data values are included in the box portion ? What percent are included in each of the “whiskers” on the ends of the box?

Answers

1. Answer :

Given Data :

4.3,  5.1,  3.9,  4.5,  4.4,  4.9,  5.0,  4.7,  4.1,  4.6,  4.4,  4.3, 4.8,  4.4,  4.2,  4.5,  4.4

Step 1 :

Let us write the observations in the data in ascending order. 

3.9,  4.1,  4.2,  4.3,  4.3,  4.4,  4.4,  4.4,  4.4,  4.5,  4.5,  4.6,  4.7,  4.8,  4.9,  5.0,  5.1

Step 2 :

Number of observations (n) = 17.

Let us find lower quartile, upper quartile and median.

Lower Quartile :

To find the lower quartile, find the value of ⁽ⁿ ⁺ ¹⁾⁄₄.

= ⁽ⁿ ⁺ ¹⁾⁄₄

= ⁽¹⁷ ⁺ ¹⁾⁄₄

= ¹⁸⁄₄

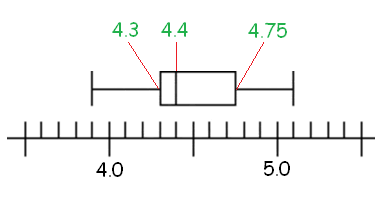
= 4.5

Lower quartile comes in between 4^th and 5^th observations.

So, lower quartile is equal to average of 4^th and 5^th observations.

Lower quartile :

= ⁽⁴^.³ ⁺ ⁴^.³⁾⁄₂

= ⁸^.⁶⁄₂

= 4.3

Upper Quartile :

To find the upper quartile, find the value of ³⁽ⁿ ⁺ ¹⁾⁄₄.

= ³⁽ⁿ ⁺ ¹⁾⁄₄

= ³⁽¹⁷ ⁺ ¹⁾⁄₄

= ⁵⁴⁄₄

= 13.5

Upper quartile comes in between 13^th and 14^th observations.

So, upper quartile is equal to average of 13^th and 14^th observations.

Upper quartile :

= ⁽⁴^.⁷ ⁺ ⁴^.⁸⁾⁄₂

= ⁹^.⁵⁄₂

= 4.75

Median :

To find the upper quartile, find the value of ⁽ⁿ ⁺ ¹⁾⁄₂.

= ⁽ⁿ ⁺ ¹⁾⁄₂

= ⁽¹⁷ ⁺ ¹⁾⁄₂

= ¹⁸⁄₂

= 9

Median is exactly the 9^th observation. 

So, median = 4.4.

Step 3 :

Using lower quartile, upper quartile and median, we can make box-plot graph as given below. 

2. Answer :

Part (i) :

Given Data :

Step 1 :

Order the data and find the needed values.

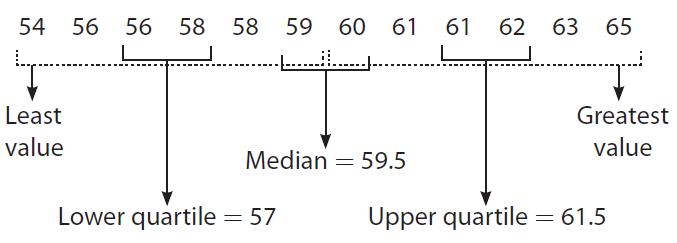
Step 2 :

Draw the box-plot.

Draw a number line that includes all the data values.

On the number line, draw dots above the least value, the lower quartile, the median, the upper quartile, and the greatest value.

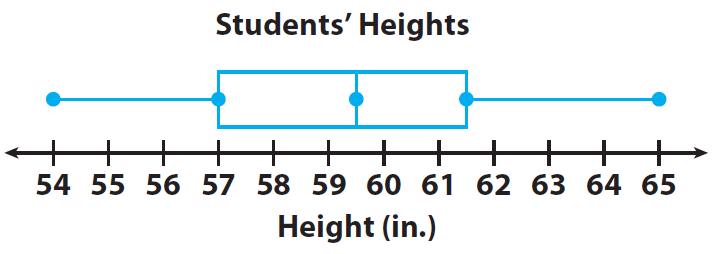
Part (ii) :

50%, 25%, 25%

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.