FACTORING TRINOMIALS BOX METHOD
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Factoring using the 'box' method is a good alternative method factoring trinomials by grouping method, when the leading coefficient, 'a' is not equal to 1 or -1.
That is, in a trinomial in the form (ax2 + bx + c),
a ≠ 1 or -1
Before we follow the steps below, we have to make sure to first take out common factors among the coefficients of the trinomial. Otherwise, the method will not work and therefore will give us a wrong answer.
In other words, for this to work, the Greatest Common Factor (GCF) of a, b, and c in (ax2 + bx + c) must be 1.
Steps to Factor a Trinomial Using the Box Method
Step 1 :
Multiply the leading coefficient and the constant term (number without variable).
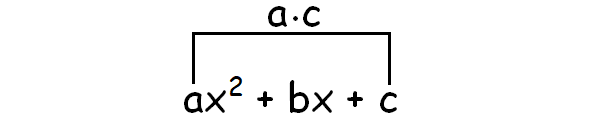
Step 2 :
Find two numbers such that the product is equal to a ⋅ c and the sum is equal to the middle coefficient, b. Let 'm' and 'n' be the two numbers satisfying the two conditions.
Step 3 :
Create a 2x2 grid and place the following terms in the right boxes:
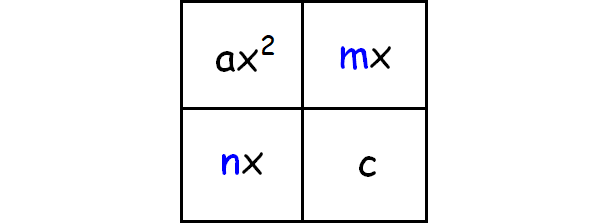
∙ Place the first term in the upper left box.
∙ Place the constant term in the lower right box.
∙ Place the numbers you found in step 2 in the remaining empty boxes. This time, it doesn’t matter where you place them. Make sure that you attach a variable x to each number.
Step 4 :
Find the greatest common factor on each row and column. Place them outside the box. Take the sign of the term closest to it.
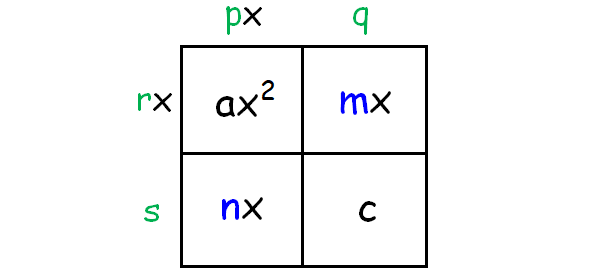
where p, q, r and s are the greatest common factors of the coefficients.
Step 5 :
The factors of the trinomial are coming from the outside terms.
ax2 + bx + c = (px + q)(rx + s)
Example 1 :
Factor
3x2 + 19x + 6
Solution :
Step 1 :
Draw a box, split it into four parts.
Write the first and last term in the first and last box respectively.
Step 2 :
Multiply the coefficient of x2 by the last term and find the factors of this number.
When we combine the two factors, we should get the middle term.
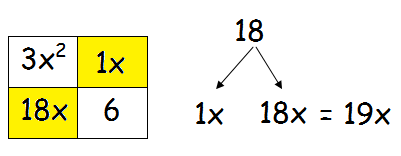
Step 3 :
Factor horizontally and vertically.
Horizontally :
|
Factor x from the 1st row 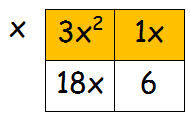 |
Factor 6 from the 2nd row 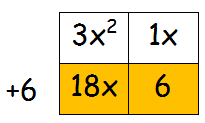 |
Vertically :
|
Factor 3x from the 1st column 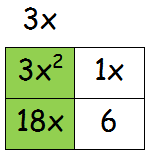 |
Factor 1 from the 2nd column 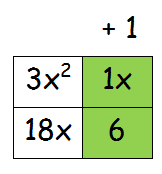 |
3x2 + 19x + 6 = (x + 6)(3x + 1)
So, the factors of the given trinomial are
(x + 6) and (3x + 1)
Example 2 :
Factor :
5y2 - 29y + 20
Solution :
Step 1 :
Draw a box, split it into four parts.
Write the first and last term in the first and last box respectively.
Step 2 :
Multiply the coefficient of y2 by the last term and find the factors of this number. When we combine the two factors, we should get the middle term.
Since the middle term is negative, both factors will have negative sign.

Step 3 :
Factor horizontally and vertically
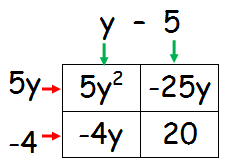
5y2 - 29y + 20 = (5y - 4)(y - 5)
So, the factors of the given trinomial are
(5y - 4) and (y - 5)
Example 3 :
Factor :
2x2 + 17x - 30
Solution :
Step 1 :
Draw a box, split it into four parts.
Write the first and last term in the first and last box respectively.
Step 2 :
Multiply the coefficient of x2 by the last term and find the factors of this number. When we combine the two factors, we should get the middle term.
Since the last term is negative, the factors will be in the combination of positive and negative.
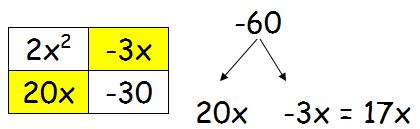
Step 3 :
Factor horizontally and vertically
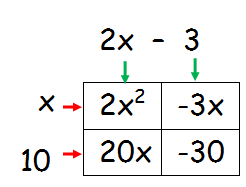
2x2 + 17x - 30 = (x + 10)(2x - 3)
So, the factors of the given trinomial are
(x + 10) and (2x - 3)
Example 4 :
Factor :
18x2 - x - 4
Solution :
Step 1 :
Draw a box, split it into four parts.
Write the first and last term in the first and last box respectively.
Step 2 :
Multiply the coefficient of x2 by the last term and find the factors of this number. When we combine the two factors, we should get the middle term.
Since the middle and last term are negative, the factors will be in the combination of positive and negative.
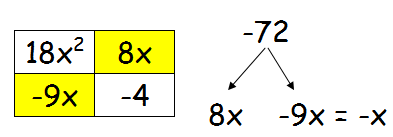
Step 3 :
Factor horizontally and vertically
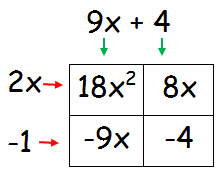
18x2 - x - 4 = (2x - 1)(9x + 4)
So, the factors of the given trinomial are
(2x - 1) and (9x + 4)
Example 5 :
Factor :
42 + a - a2
Solution :
= 42 + a - a2
Writing the given trinomial in standard form, we get
= -(a2 - a - 42)
= -(a2 + 7a - 6a - 42)
= -[a (a + 7) - 6(a + 7)]
= -[(a - 6) (a + 7)]
= -(a - 6)(a + 7)
So, the factored form is -(a - 6)(a + 7).
Example 6 :
Factor :
9x3- 24x2 + 16x
Solution :
= 9x3- 24x2 + 16x
Factoring x, we get
= x(9x2- 24x + 16)
= x(9x2- 12x - 12x + 16)
= x[3x(3x - 4) - 4(3x - 4)]
= x(3x - 4)(3x - 4)
So, the factored form is x(3x - 4)(3x - 4).
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 40)
Dec 25, 25 08:30 AM
10 Hard SAT Math Questions (Part - 40) -
10 Hard SAT Math Questions (Part - 41)
Dec 24, 25 07:58 PM
10 Hard SAT Math Questions (Part - 41) -
ASTC Formula in Trigonometry
Dec 23, 25 11:34 PM
ASTC Formula in Trigonometry - Concepts - Examples and Solved Problems


