BOX AND WHISKER PLOT

Box and whisker-plot is the graph used in statistics to represent the central 50% of the values of a data set. 

The picture figure given below clearly illustrates this. 

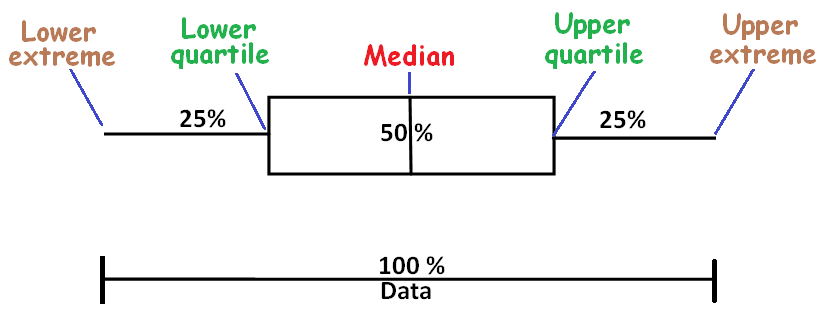
In the above figure, the box spans interquartile range (central 50%).

To draw box and whisker-plot graph for a data set, we have to know lower quartile, upper quartile and median.  

Steps to Construct Box and Whisker Plot

To construct box and whisker-plot for the given data set, we have to do the following steps. 

Step 1 : 

Write the observations of the given data set in ascending order. 

Step 2 : 

Find lower quartile, upper quartile and median using the formulas given below. 

Lower quartile  =  (n + 1)/4

Upper quartile  =  3(n + 1)/4

Median  =  (n + 1)/2

Here, n  =  number of observations in the given data set. 

Step 3 : 

Using lower quartile, upper quartile and median, we have to construct box and whisker-plot as given in the above picture.

Example

Construct box and whisker-plot for the data given below. 

4.3,  5.1,  3.9,  4.5,  4.4,  4.9,  5.0,  4.7,  4.1,  4.6,  4.4,  4.3,  4.8,  4.4,  4.2,  4.5,  4.4

Construction of box and whisker-plot :

Step 1 : 

Let us write the observations in the data in ascending order. 

3.9,  4.1,  4.2,  4.3,  4.3,  4.4,  4.4,  4.4,  4.4,  4.5,  4.5,  4.6,  4.7,  4.8,  4.9,  5.0,  5.1

Step 2 : 

Number of observations (n)  =  17

Let us find lower quartile, upper quartile and median.

Lower Quartile : 

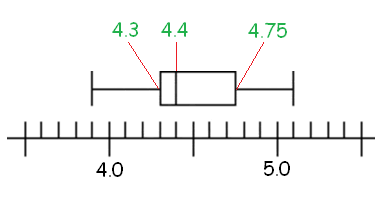
Lower quartile  =  (n + 1)/4  =  (17 + 1)/4  =  18/4  =  4.5

Lower quartile comes in between 4th and 5th observations.

So, lower quartile  = average of 4th and 5th observations

Lower quartile  =  (4.3 + 4.3)/2  =  8.6/2  =  4.3

Upper Quartile : 

Upper quartile  =  3(n+1)/4  =  3(17 + 1)/4  =  54/4  =  13.5

Upper quartile comes in between 13th and 14th observations.

So, upper quartile  = average of 13th and 14th observations

Upper quartile  =  (4.7 + 4.8)/2  =  9.5/2  =  4.75

Median : 

Median  =  (n + 1)/2  =  (17 + 1)/2  =  18/2  =  9

Median is exactly the 9th observation. 

So, median  =  4.4

Step 3 : 

Using lower quartile, upper quartile and median, we can construct box and whisker-plot graph as shown below. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.