BISECTORS OF A TRIANGLE

In a triangle, bisector is the line which divides a side of the triangle into two equal halves. In other words, the bisector will always intersect at the mid points of a side of the triangle.

Perpendicular Bisector of a Triangle :

In a triangle, perpendicular bisector is a line (or ray or segment) that is perpendicular to a side of the triangle at the midpoint of the side.

When three or more lines (or rays or segments) intersect in the same point, they are called concurrent lines (or rays or segments).

The point of intersection of the lines is called the point of concurrency. In any triangle, the three perpendicular bisectors are concurrent. The point of concurrency can be inside the triangle, on the triangle, or outside the triangle as shown in the diagram below.

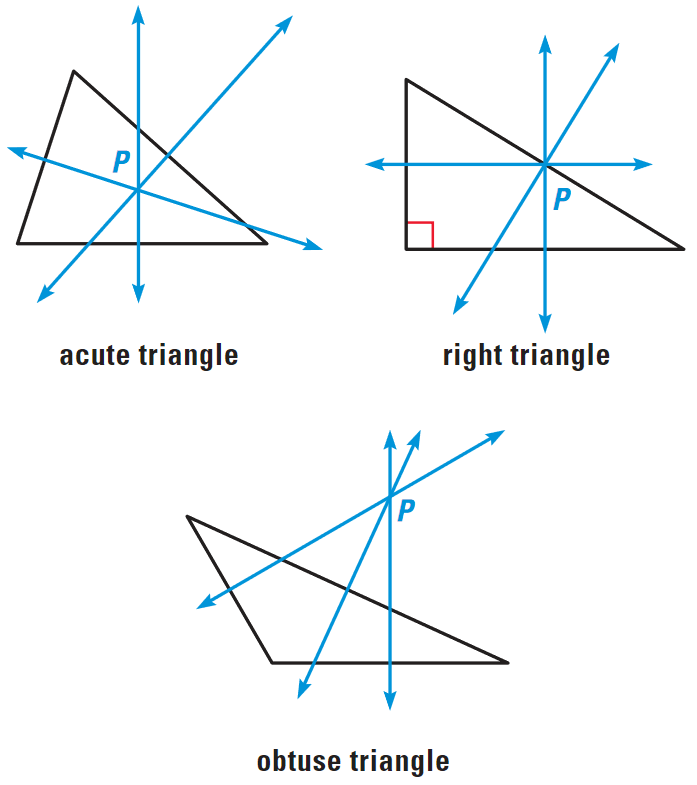
The point of concurrency of the perpendicular bisectors in a triangle is called the circumcenter of the triangle.

Angle Bisector of a Triangle :

In a triangle, an angle bisector is a line which bisects an angle of the triangle.

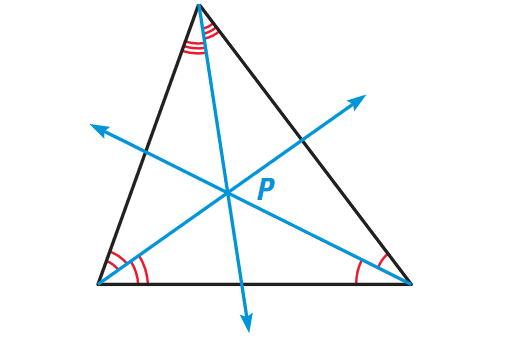
The three angle bisectors are concurrent. The point of concurrency of the angle bisectors is called the incenter of the triangle and it always lies inside the triangle.

It has been illustrated in the diagram shown below.

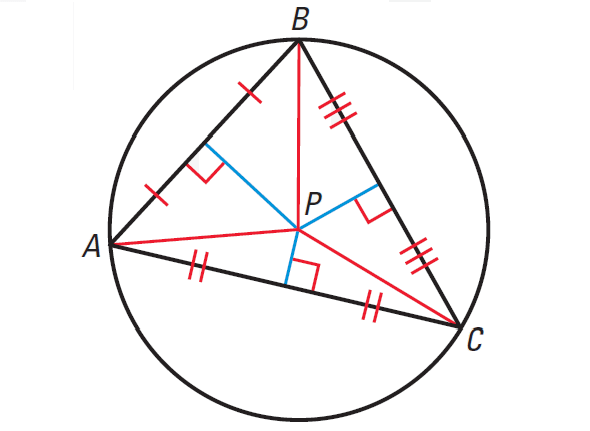
Concurrency of Perpendicular Bisectors of a Triangle

In a triangle, the perpendicular bisectors intersect at a point that is equidistant from the vertices of the triangle.

PA = PB = PC

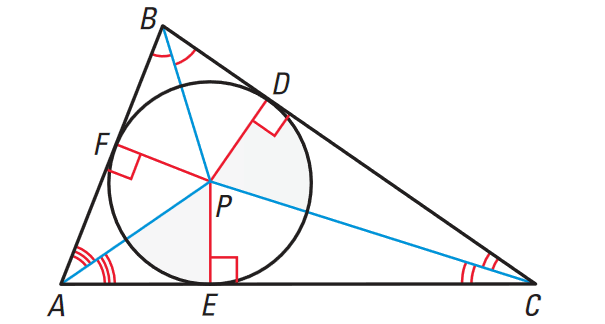
Concurrency of Angle Bisectors of a Triangle

In a triangle, the angle bisectors intersect at a point that is equidistant from the sides of the triangle.

PD = PE = PF

Solved Examples

Example 1 :

Construct a perpendicular bisector to a line segment.

Solution :

Step 1 :

Draw the line segment AB.

Step 2 :

With the two end points A and B of the line segment as centers and more than half the length of the line segment as radius draw arcs to intersect on both sides of the line segment at C and D.

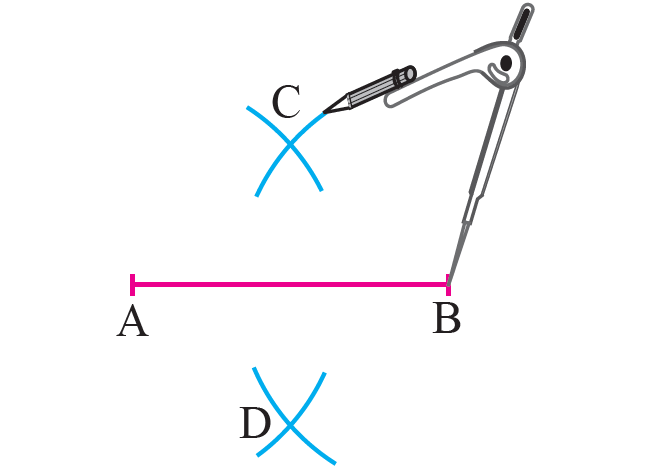
Step 3 :

Join C and D to get the perpendicular bisector of the given line segment AB.

In the diagram above, CD is the perpendicular bisector of the line segment AB.

Example 2 :

Construct the circumcenter of the triangle ABC with AB = 5 cm, ∠A = 70° and ∠B = 70°.

Solution :

Step 1 :

Draw triangle ABC with the given measurements.

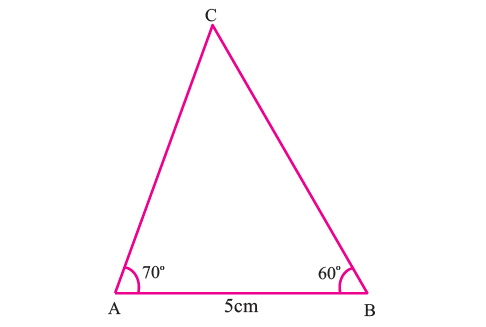
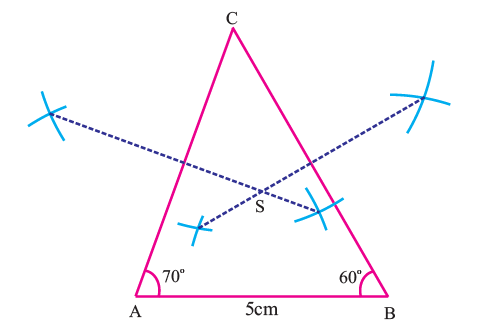
Step 2 :

Construct the perpendicular bisectors of any two sides (AC and BC) and let them meet at S which is the circumcenter.

Example 3 :

A company plans to build a distribution center that is convenient to three of its major clients as shown in the diagram below.

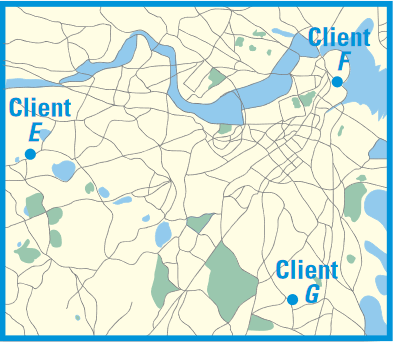
The planners start by roughly locating the three clients on a sketch and finding the circumcenter of the triangle formed.

(i) Explain why using the circumcenter as the location of a distribution center would be convenient for all the clients.

(ii) Make a sketch of the triangle formed by the clients. Locate the circumcenter of the triangle. Tell what segments are congruent.

Solution (i) :

Because the circumcenter is equidistant from the three vertices, each client would be equally close to the distribution center.

Solution (ii) :

Label the vertices of the triangle as E, F, and G. Draw the perpendicular bisectors. Label their intersection as D.

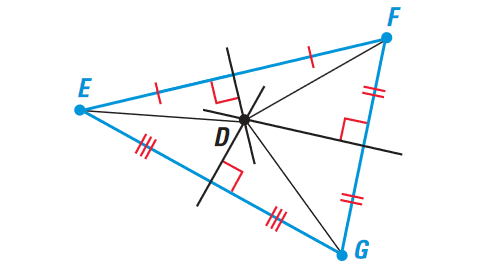
By theorem 1 given above, in a triangle, the perpendicular bisectors intersect at a point that is equidistant from the vertices of the triangle.

So, 

DE = DF = DG

Example 4 :

In the diagram shown below, the angle bisectors of ΔMNP meet at point L.

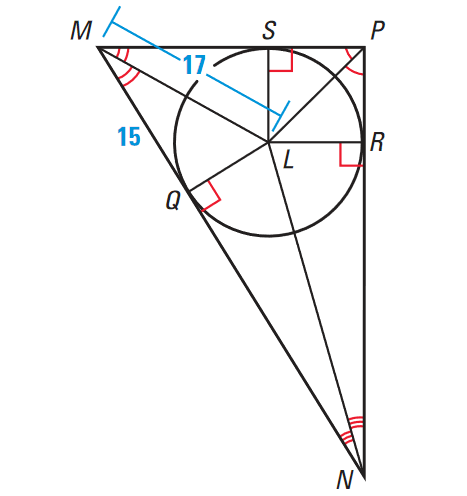
(i) What segments are congruent?

(ii) Find LQ and LR

Solution (i) :

By theorem "Concurrency of Angle Bisectors of a Triangle", the three angle bisectors of a triangle intersect at a point that is equidistant from the sides of the triangle.

So, we have

LR ≅ LQ ≅ LS

Solution (ii) :

By theorem "Concurrency of Angle Bisectors of a Triangle", the three angle bisectors of a triangle intersect at a point that is equidistant from the sides of the triangle.

Use the Pythagorean Theorem to find LQ in ΔLQM.

LQ² + MQ² = LM²

Substitute MQ = 15 and LM = 17.

LQ² + 15² = 17²

Simplify. 

LQ² + 225 = 289

Subtract 225 from both sides.

LQ² = 64

LQ² = 8²

LQ = 8 units

Because LR ≅ LQ,

LR = 8 units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.