BISECTORS OF A TRIANGLE WORKSHEET

Problem 1 :

Construct a perpendicular bisector to a line segment.

Problem 2 :

Construct the circumcenter of the triangle ABC with AB = 5 cm, ∠A = 70° and ∠B =  70°.

Problem 3 :

A company plans to build a distribution center that is convenient to three of its major clients as shown in the diagram below.

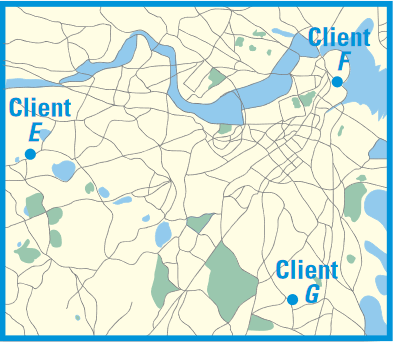
The planners start by roughly locating the three clients on a sketch and finding the circumcenter of the triangle formed.

(i) Explain why using the circumcenter as the location of a distribution center would be convenient for all the clients.

(ii) Make a sketch of the triangle formed by the clients. Locate the circumcenter of the triangle. Tell what segments are congruent.

Problem 4 :

In the diagram shown below, the angle bisectors of ΔMNP meet at point L.

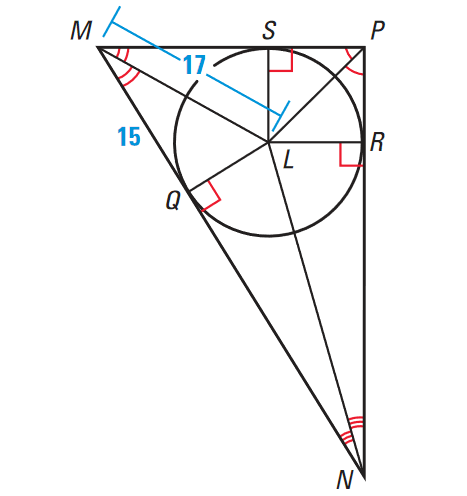
(i) What segments are congruent?

(ii) Find LQ and LR

1. Answer :

Step 1 :

Draw the line segment AB.

Step 2 :

With the two end points A and B of the line segment as centers and more than half the length of the line segment as radius draw arcs to intersect on both sides of the line segment at C and D.

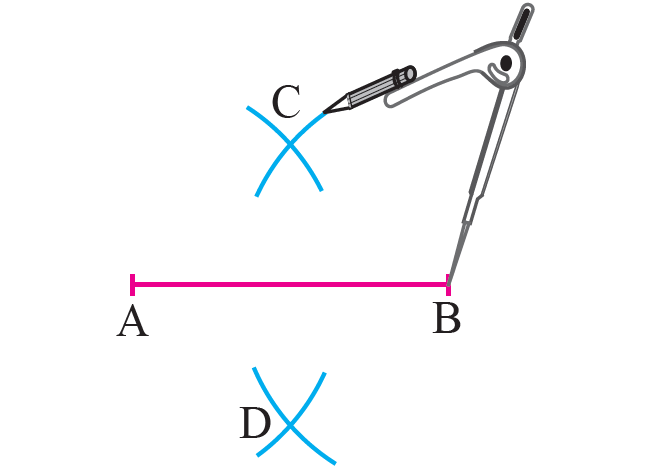
Step 3 :

Join C and D to get the perpendicular bisector of the given line segment AB.

In the diagram above, CD is the perpendicular bisector of the line segment AB.

2. Answer :

Step 1 :

Draw triangle ABC with the given measurements.

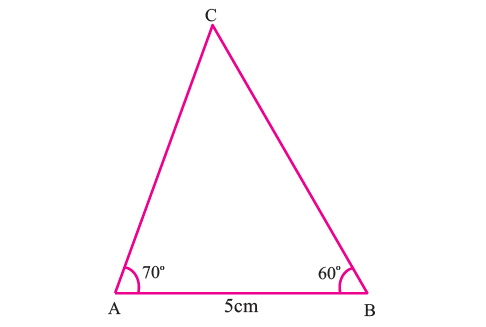
Step 2 :

Construct the perpendicular bisectors of any two sides (AC and BC) and let them meet at S which is the circumcenter.

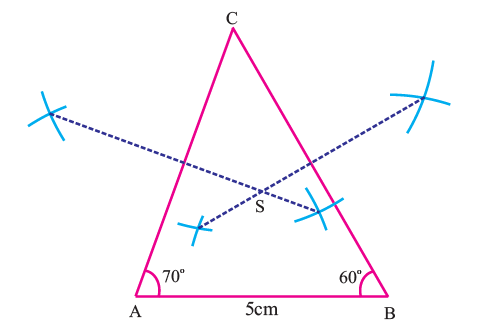
3. Answer :

Part (i) :

Because the circumcenter is equidistant from the three vertices, each client would be equally close to the distribution center.

Part (ii) :

Label the vertices of the triangle as E, F, and G. Draw the perpendicular bisectors. Label their intersection as D.

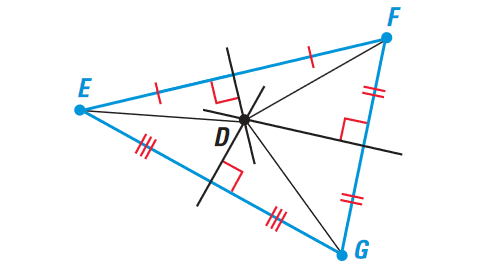
By theorem 1 given above, in a triangle, the perpendicular bisectors intersect at a point that is equidistant from the vertices of the triangle.

So,

DE = DF = DG

4. Answer :

Part (i) :

By theorem "Concurrency of Angle Bisectors of a Triangle", the three angle bisectors of a triangle intersect at a point that is equidistant from the sides of the triangle.

So, we have

LR ≅ LQ ≅ LS

Part (ii) :

By theorem "Concurrency of Angle Bisectors of a Triangle", the three angle bisectors of a triangle intersect at a point that is equidistant from the sides of the triangle.

Use the Pythagorean Theorem to find LQ in ΔLQM.

LQ² + MQ² = LM²

Substitute MQ = 15 and LM = 17.

LQ² + 15² = 17²

Simplify.

LQ² + 225 = 289

Subtract 225 from both sides.

LQ² = 64

LQ² = 8²

LQ = 8 units

Because LR ≅ LQ,

LR = 8 units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.